Крутящий момент и мощность двигателя особенности и нюансы
Рассуждая о главнейшем автомобильном узле — двигателе, стало принято превозносить мощность превыше других параметров. Между тем, вовсе не мощностные способности являются первостепенной характеристикой силовой установки, а явление, называемое крутящим моментом. Потенциал любого автомобильного двигателя напрямую определяется данной величиной.
Понятие крутящего момента ДВС. О сложном простыми словами
Крутящим моментом применительно к двигателям автомобилей называется произведение значения силы и плеча рычага, или, простыми словами, сила давления поршня на шатун. Исчисляется эта сила ньютон-метрами, и чем выше ее величина, тем резвее машина.


Более того, мощность двигателя, выражаемая в ваттах, — это не что иное, как умноженное на частоту вращения коленвала значение крутящего момента в ньютон-метрах.
Представим лошадь, которая тащит тяжелые сани и увязает в канаве. Вытянуть сани не получится, если лошадь будет пытаться выскочить из канавы с разбега. Здесь необходимо приложить определенную силу, которая и будет являться крутящим моментом (КМ).
Часто крутящий момент путают с частотой вращения коленвала. В реальности это два совершенно разных понятия. Если вернуться к примеру с лошадью, застрявшей в канаве, частота шага будет символизировать частоту оборотов двигателя, тогда как сила, прикладываемая животным при отталкивании во время шага, олицетворяет в данном случае крутящий момент.
Факторы, влияющие на величину крутящих моментов
Из примера с лошадью легко догадаться, что в данном случае значение КМ будет во многом определяться мышечной массой животного. Применительно к автомобильному двигателю внутреннего сгорания эта величина зависит от рабочего объема силовой установки, а также от:
- уровня рабочего давления внутри цилиндров;
- размера поршня;
- диаметра кривошипа коленвала.
Наиболее сильно крутящий момент зависим от рабочего объема и давления внутри силовой установки, и эта зависимость прямо пропорциональна. Другими словами, двигатели с большим объемом и давлением, соответственно, отличаются и большим моментом.
Прямая зависимость наблюдается также между КМ и радиусом кривошипа коленвала. Однако конструкция современных автомобильных двигателей такова, что не позволяет варьировать значения момента в широких пределах, из-за чего возможности добиться повышенного крутящего момента за счет радиуса кривошипа коленчатого вала у конструкторов ДВС невелики. Вместо этого разработчики прибегают к таким способам увеличить момент, как использование технологий турбонаддува, увеличение степени сжатия, оптимизация процесса сгорания топлива, использование впускных коллекторов специальных конструкций, и т.д.
Важно, что КМ увеличивается с ростом оборотов двигателя, однако после достижения максимума на определенном диапазоне крутящий момент понижается несмотря на продолжающийся прирост частоты вращения коленвала.
Влияние крутящего момента ДВС на характеристики автомобиля
Величина крутящего момента выступает тем самым фактором, который непосредственным образом задает динамику разгона автомобиля. Если вы — заядлый автолюбитель, то могли заметить, что разные автомобили, но с одинаковым силовым агрегатом, по-разному ведут себя на дороге. Или на порядок менее мощный автомобиль на дороге превосходит того, у которого под капотом лошадиных сил больше, причем даже тогда, когда сравнимые авто имеют одинаковые размеры и вес. Причина заключается как раз в разнице в крутящих моментах.
Лошадиные силы можно представить как индикатор выносливости мотора. Именно этот показатель определяет скоростные возможности автомобиля. Но поскольку крутящий момент является разновидностью силы, то непосредственно от его величины, а не от количества «лошадей», зависит то, насколько быстро автомобиль сможет достичь максимального скоростного режима. По этой причине далеко не каждое мощное авто обладает хорошей динамикой разгона, а те, что способны разгоняться быстрее других, необязательно оснащены мощным двигателем.
Вместе с тем высокий крутящий момент еще не гарантирует сам по себе отличную динамичность машины. Ведь кроме прочего, динамика увеличения скорости, а также способность авто к резвому преодолению подъемов участков, зависит от диапазона работы силовой установки, передаточных чисел трансмиссии, отзывчивости педали газа. Наряду с этим нужно учитывать, что момент существенно понижается из-за различных противодействующих явлений — сил качения колес и трения в различных автомобильных узлах, из-за аэродинамических и прочих явлений.
Крутящий момент vs. мощность. Связь с динамикой автомобиля
Мощность — производное такого явления, как крутящий момент, ею выражается работа силовой установки, выполненная за определенное время. А поскольку КМ олицетворяет собой непосредственную работу мотора, то в виде мощности отражается величина момента в соответствующий период времени.
Наглядно увидеть связь между мощностью и КМ позволяет следующая формула:
P=М*N/9549
Где: P в формуле означает мощность, М — крутящий момент, N — обороты двигателя за минуту, а 9549 — коэффициент обращения N в радианы в секунды. Результатом вычислений по данной формуле будет являться число в киловаттах. Когда нужно перевести полученный результат в лошадиные силы, полученное число умножают на 1.36.
По сути, крутящим моментом является мощность при неполных оборотах, например, во время обгона. Мощность возрастает по мере роста момента, и чем выше этот параметр, тем больше запас кинетической энергии, тем легче автомобиль преодолевает противодействующие на него силы и тем лучше его динамические характеристики.
При этом важно помнить, что мощность достигает своих максимальных значений не сразу, а постепенно. Ведь с места автомобиль трогается на минимуме оборотов, и затем скорость наращивается. Именно здесь и подключается сила под названием крутящий момент, и именно она определяет тот самый временной отрезок, за который авто достигнет своей пиковой мощности, или, другими словами, скоростную динамику.
Из этого следует, что машина с силовым агрегатом мощнее, но обладающим недостаточно высоким крутящим моментом, уступит по скорости разгона модели с мотором, который, напротив, не способен похвастать хорошей мощностью, но превосходит конкурента в крутящем моменте. Чем большая тяга, сила передается ведущим колесам и чем богаче диапазон оборотов силовой установки, в котором достигается высокий КМ, тем быстрее происходит ускорение автомобиля.
В то же время существование крутящего момента возможно без мощности, но существование мощности без момента — нет. Представьте, что наша лошадь с санями увязла в грязи. Производимая лошадью мощность в этот момент будет равняться нулю, но крутящий момент (попытки выбраться, тяга), хотя его может быть недостаточно для движения, будет присутствовать.
Дизельный момент. Отличия между КМ бензинового и дизельного двигателей
Если сравнивать бензиновые силовые установки с дизельными, то отличительной особенностью последних (всех без исключения) является повышенный крутящий момент при меньшем количестве лошадиных сил.

Бензиновый ДВС достигает своих максимальных значений КМ при трех-четырех тысячах оборотов в минуту, но затем способен стремительно нарастить мощность, раскрутившись за минуту до семи-восьми тысяч раз. Диапазон оборотов же коленчатого вала дизельного двигателя обычно ограничен тремя-пятью тысячами. Однако в дизельных установках больше ход поршня, выше уровень сжатия и другая специфика сгорания топлива, что обеспечивает не только более высокий относительно бензиновых установок крутящий момент, но и доступность этой силы едва ли не с холостого хода.
По этой причине смысла добиваться повышенной мощности дизельных двигателей нет: уверенная, доступная «с низов» тяга, высокий коэффициент полезного действия и топливная эффективность полностью нивелируют отставание таких ДВС от бензиновых как по мощностным показателям, так и по скоростному потенциалу.
Особенности правильного разгона машины. Как выжать из авто максимум
Основа правильного разгона — умение работать с коробкой передач и следование принципу «от максимума момента до пика мощности». То есть, добиться наилучшей динамики разгона машины можно только поддерживая частоту вращения коленвала в том диапазоне значений, при которых КМ достигает своего максимума. Очень важно, чтобы обороты совпали с пиком крутящего момента, но при этом должен оставаться запас по их увеличению. Если разгоняться на оборотах выше пиковой мощности, динамика разгона будет меньше.
Диапазон оборотов, соответствующий максимуму крутящего момента, обусловлен характеристиками двигателя.
Выбор двигателя. Какой лучше — с высоким моментом или повышенной мощностью?
Если подвести итоговую черту под всем вышесказанным, то станет очевидно, что:
- крутящий момент — ключевой фактор, характеризующий возможности силовой установки;
- мощность — это производная КМ и, соответственно, вторичная характеристика двигателя;
- прямую зависимость мощности от момента можно увидеть по выведенной физиками формуле Р (мощность) = М (момент) * n (частота вращения коленвала в минуту).
Таким образом, выбирая между двигателем с большим количеством лошадиных сил, но меньшим крутящим моментом, и двигателем с большим КМ, но меньшей мощностью, приоритетным будет второй вариант. Использовать весь заложенный в автомобиль потенциал позволит только такой мотор.
При этом не следует забывать о взаимосвязи динамических характеристик автомобиля с такими факторами, как отзывчивость педали газа и коробка переключения передач. Лучшим вариантом станет то авто, которое не только оснащено двигателем с высоким крутящим моментом, но и имеет наименьшую длину задержки между нажатием педали газа и реакцией двигателя, а также трансмиссию с короткими соотношениями передач. Наличие этих особенностей компенсирует маломощность силовой установки, заставляя автомобиль разгоняться быстрее, чем машина с двигателем похожей конструкции, но с меньшей силой тяги.
Видео: Мощность и крутящий момент двигателя
Видео: Крутящий момент, обороты и мощность двигателя. Простыми словами
Вконтакте
Google+
Что такое мощность двигателя и крутящий момент. Как рассчитать мощность мотора
Мощность двигателя – это величина, показывающая, какую работу способен совершить мотор в единицу времени. То есть то количество энергии, которую двигатель передает на трансмиссию за определенный временной промежуток. Измеряется в киловаттах (кВт) или лошадиных силах (л. с.).

Как рассчитывается мощность двигателя?
Расчет мощности мотора проводится несколькими способами. Самый доступный способ – через крутящий момент. Умножаем крутящий момент на угловую скорость – получаем мощность двигателя.
N_дв=M∙ω=2∙π∙M∙n_дв
где:
N_дв – мощность двигателя, кВт;
M – крутящий момент, Нм;
ω – угловая скорость вращения коленчатого вала, рад/сек;
π – математическая постоянная, равная 3,14;
n_дв – частота вращения двигателя, мин-1.
Мощность рассчитывается и через среднее эффективное давление. Камера сгорания имеет определенный объем. Разогретые газы воздействуют на поршень в цилиндре с определенным давлением. Двигатель вращается с некоторой частотой. Произведение объема двигателя, среднего эффективного давления и частоты вращения, поделенное на 120, и даст теоретическую мощность двигателя в кВт.
N_дв=(V_дв∙P_эфф∙n_дв)/120
где:
V_дв – объем двигателя, см3;
P_эфф – эффективное давление в цилиндрах, МПа;
120 – коэффициент, применяемый для расчета мощности четырехтактного двигателя (у двухтактных ДВС этот коэффициент равен 60).
Для расчета лошадиных сил киловатты умножаем на 0,74.
N_(дв л.с.)=N_дв∙0,74
где:
N_дв л.с. – мощность двигателя в лошадиных силах, л. с.
Другие формулы мощности двигателя используются в реальных расчетах реже. Эти формулы включают в себя специфичные переменные. И чтобы измерить мощность двигателя по другим методикам, нужно знать производительность форсунок или массу потребленного двигателем воздуха.
На практике расчет мощности автопроизводители выполняют эмпирическим способом, то есть замеряют на стенде и строят график зависимости по факту, на основании полученных во время испытаний показателей.
Мощность двигателя – величина непостоянная. Для каждого мотора есть кривая, которая отображает на графике зависимость мощности от частоты вращения коленчатого вала. До определенного пика, примерно до 4-5 тысяч оборотов, мощность растет пропорционально оборотам. Далее идет плавное отставание роста мощности, кривая наклоняется. Примерно к 7-8 тысячам оборотов мощность идет на спад. Сказывается перекрытие клапанов на большой частоте вращения коленвала и падение КПД мотора из-за недостаточно интенсивного газообмена.
Чтобы узнать мощность двигателя, обратитесь к инструкции по эксплуатации авто. В разделе с техническими характеристиками мотора будет указана мощность и обороты, при которых она достигает пикового значения. Если мощность указана киловаттах, чтобы рассчитать лошадиные силы двигателя, воспользуйтесь приведенной выше формулой. В некоторых случаях автопроизводитель предоставляет график, на котором есть зависимость мощности двигателя и крутящего момента от частоты оборотов.
Видео: Простыми словами без сложных формул и расчетов, что такое мощность, крутящий момент и обороты двигателя.
Мощность ДВС определяет, насколько быстро автомобиль способен передвигаться или ускоряться (совершать работу). Полезная мощность двигателя рассчитывается с учетом потерь в трансмиссии, то есть указывает, сколько от изначальной мощности мотора по факту доходит до колес авто.
Что такое крутящий момент
Крутящий момент в двигателе автомобиля – это вращающая сила, которая численно равна произведению приложенной силы (давление раскаленных газов на поршень) на плечо (расстояние между осями коренных и шатунных шеек коленчатого вала в проекции, перпендикулярной оси вращения коленвала). Измеряется крутящий момент в ньютонах на метр (Нм).
Крутящий момент ДВС зависит от силы давления на поршень и расстояния между коренными и шатунными шейками. Зависимость здесь прямая. Чем больше плечо и чем больше давление на поршень – тем больше крутящий момент двигателя.
У дизельных двигателей степень сжатия больше. Больше и ход поршня в цилиндре (при равном с бензиновым мотором диаметре цилиндров). А это значит, что и расстояние между коренными и шатунными шейками будет больше. То есть длиннее плечо. За счет большей степени сжатия при рабочем такте у дизелей выше сила, давящая на поршень. Крутящий момент в дизельных моторах при прочих равных больше, чем в бензиновых.
Крутящий момент влияет на то, сколько энергии отдает мотор в текущий момент времени. Крутящий момент есть та величина, которая определяет фактически передаваемую в данный момент времени энергию на трансмиссию. Чем больше момент, тем сильнее тяга двигателя при текущих оборотах.
Что лучше: мощность или крутящий момент
Мощность и крутящий момент двигателя – величины взаимосвязанные. Это хорошо видно в формуле из первого пункта.
Пик крутящего момента на графике зависимости от частоты вращения мотора появляется раньше, чем пик мощности. Это справедливо как для дизельных, так и для бензиновых моторов. Однако у дизелей крутящий момент достигается раньше, и плато (интервал частоты вращения при пиковом значении) длиннее. У бензиновых ДВС мощность выше, хотя для ее достижения нужно раскрутить мотор почти до максимальных оборотов.
Сказать определенно, что лучше: мощность или крутящий момент, нельзя. Все зависит от случая. Трансмиссия современного авто способна трансформировать эти величины под требуемые условия. Поясним на примерах.
Для тяжелой техники, которой важна тяга в широком диапазоне оборотов, важнее крутящий момент. Мотор должен хорошо тянуть. Раскручивать его до предельных оборотов не нужно. Отчасти поэтому почти вся коммерческая техника оснащается дизельными моторами.
В гоночных автомобилях важнее мощность. Моторы этих авто по оборотам пилоты во время заездов держат в красной зоне. Двигатель отдает максимальную мощность. А трансмиссия преобразовывает мощность в тягу.
Для гражданских авто важен стиль вождения. Для езды на автомате подойдут оба мотора. Автоматическая трансмиссия будет держать мотор в диапазоне оборотов, при которых двигатель отдает максимум своего потенциала.

Для агрессивной езды на механике с раскручиванием двигателя в красную зону тахометра лучше подойдет бензиновый мотор. Но в этом случае нужно понимать, что для получения максимальной производительности от мотора потребуется держать его на пике оборотов и часто переключать передачи. Пик мощности у бензинового ДВС имеет малый диапазон и находится около максимальных оборотов. Для уверенных обгонов и ускорений нужно будет понижать передачу и раскручивать двигатель.
Для размеренной езды, особенно в городе, больше подходит дизель. Для обгона на дизельном авто зачастую не потребуется переходить на пониженную передачу, а высокий крутящий момент в широком диапазоне оборотов позволит реже переключаться.
topmekhanik.ru
Крутящий момент — что это такое?
 Автолюбители постоянно спорят о том, чей двигатель мощнее, но не все знают, из чего складывается этот параметр.Всем знакомый термин «лошадиная сила» был предложен изобретателем Джеймсом Уаттом в восемнадцатом веке. Идея появилась у изобретателя, пока он наблюдал за лошадью, запряженной в машину, поднимавшую уголь из шахты.
Автолюбители постоянно спорят о том, чей двигатель мощнее, но не все знают, из чего складывается этот параметр.Всем знакомый термин «лошадиная сила» был предложен изобретателем Джеймсом Уаттом в восемнадцатом веке. Идея появилась у изобретателя, пока он наблюдал за лошадью, запряженной в машину, поднимавшую уголь из шахты.
Расчеты показали, что одна лошадьспособна за минутуподнять 150 кг угля на высоту 30 метров.Н•м (Ньютон-метр) — единица измерения момента силы, входящая в международную систему единиц«СИ». Лошадиная сила стала «несистемной» величиной для измерения мощности. Одна лошадиная сила равна 735,5 Вт (Ватт — системная единица измерения, названная в честь того же английского ученого). Впоследствии лошадиные силы стали применять для обозначения мощности двигателя автомобиля.
Что интересует людей, изучающих технические характеристики того или иного автомобиля? В первую очередь мощность, затем расход топлива и максимальная скорость. О крутящем моменте вспоминают редко. А зря.
Что такое крутящий момент?
Крутящий момент двигателя – это тяговая характеристика двигателя, которая в отличие от мощности дает весьма отдаленное представление об истинных возможностях автомобиля. Для того чтобы наиболее полно ответить на вопрос: «Крутящий момент что это?», необходимо, прежде всего, уяснить, что момент двигателя и момент на колесах автомобиля – это две большие разницы. Крутящий момент двигателя, будучи величиной, равной силе на плечо (Н*м) – сила давления сгоревших в двигателе газов через поршень и шатун на плечо кривошипа коленвала, показывает лишь потенциал мотора, а сам автомобиль, в конечном итоге, движет крутящий момент на колесах.
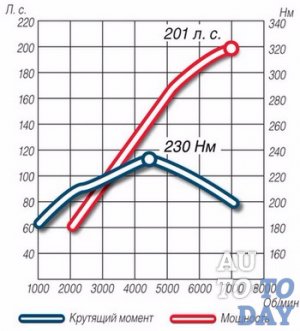
Пример №1. Суперкар мощностью 500 сил с крутящим моментом двигателя 500 Н*м и магистральная фура-тягач с отдачей 500 сил и 2500 Н*м, на колесах, тем не менее, имеют абсолютно равный крутящий момент при движении с одинаковой скоростью на оборотах максимальной мощности: М (момент на колесах, приводящий машины в движение) = N (мощность двигателя) / n (обороты колеса, при условии, что у суперкара и фуры они одинакового диаметра).
Вывод: цифра мощности отражает тягу и динамику автомобиля, а цифра крутящего момента двигателя, не учавствующая в вычислениях, может быть любой и не имеет значения.
Пример №2. Зайдем с другой стороны. Тот же суперкар и фура с вышеуказанными характеристиками (аналоги Porsche 911 GT3 RS 4.0, Scania R500 и многие другие суперкары и грузовики), как правило, имеют максимальные обороты двигателя около 9000 и 1800 соответственно. Для того чтобы компенсировать пятикратную разницу в оборотах (иметь ту же скорость движения), на фуре придется применять в пять раз более «длинную» трансмиссию, которая, соответственно, будет передавать в 5 раз меньше момента на колеса: 2500 Н*м делим на 5 и получаем те же 500 Н*м (приведенный момент), как в суперкаре.
Вывод: мы получили то же равенство тягово-динамического потенциала машин равной мощности, что и в примере №1.
Роль мощности в крутящем моменте
Мощности и крутящему моменту уделяют много внимания, ведь именно они наглядно показывают важнейшие характеристики грузового и легкового транспорта. Более того, эти цифры важны для определения поведения автомобиля в реальных условиях езды.
 Крутящий момент — показатель работы двигателя, а мощность — основной показатель выполнения этой работы. Например, редуктор может напрямую влиять на функционирование мотора. Так, пикап для большего крутящего момента способен работать на низкой передаче, к примеру, при выполнении каких-либо задач: транспортировка очень больших и тяжелых грузов. Но если Dodge RAM 1500 или Saturn SL1 поедут на одной передаче, то грузоподъемность первого будет значительно выше по причине большего числа лошадиных сил. Получается, что чем больше производится л.с., тем больше потенциал крутящего момента.
Крутящий момент — показатель работы двигателя, а мощность — основной показатель выполнения этой работы. Например, редуктор может напрямую влиять на функционирование мотора. Так, пикап для большего крутящего момента способен работать на низкой передаче, к примеру, при выполнении каких-либо задач: транспортировка очень больших и тяжелых грузов. Но если Dodge RAM 1500 или Saturn SL1 поедут на одной передаче, то грузоподъемность первого будет значительно выше по причине большего числа лошадиных сил. Получается, что чем больше производится л.с., тем больше потенциал крутящего момента.
Отметим, что это именно потенциал, который применяется в реальных условиях через трансмиссию и полуоси автомобиля. Соединение этих элементов вместе определяет, как мощность может переходить в крутящий момент.
Чтобы понять всё вышесказанное, рассмотрим отличия трактора от гоночного автомобиля.У гоночного автомобиля л.с. много, однако крутящий момент здесь нужен для увеличения скорости через редуктор. Чтобы такая машина двигалась вперед, нужно совсем немного работы, так что основная часть мощности направлена на развитие скорости.
Что касается трактора, то у него может быть мотор с таким же объемом, который вырабатывает столько же л.с. Мощность здесь необходима для работы через редуктор. Как известно, трактор не развивает высоких скоростей, но он может легко буксировать и толкать немалые грузы. Крутящий момент и мощность двигателя тесно связаны, но они выполняют абсолютно разные функции в работе легкового и грузового транспорта.
Как повысить крутящий момент?
Дорогие и сложные способы увеличения мощности и крутящего момента
 Дорогостоящие и сложные способы подразумевают внутреннее вмешательство в устройство двигателя автомобиля (технический тюнинг) и требуют значительных временных затрат на исполнение и большого опыта специалиста, осуществляющего тюнинг, а так же очень значительных финансовых вложений со стороны заказчика. При этом разница в работе двигателя автомобиля после осуществления дорогостоящего технического тюнинга будет очень ощутимой, но и заметно скажется на его моторесурсе. В дальнейшем ремонт форсированного двигателя будет сильно бить по карману, если Вам вообще удастся найти исполнителей. К дорогостоящим способам увеличения мощности и крутящего момента двигателя относятся:
Дорогостоящие и сложные способы подразумевают внутреннее вмешательство в устройство двигателя автомобиля (технический тюнинг) и требуют значительных временных затрат на исполнение и большого опыта специалиста, осуществляющего тюнинг, а так же очень значительных финансовых вложений со стороны заказчика. При этом разница в работе двигателя автомобиля после осуществления дорогостоящего технического тюнинга будет очень ощутимой, но и заметно скажется на его моторесурсе. В дальнейшем ремонт форсированного двигателя будет сильно бить по карману, если Вам вообще удастся найти исполнителей. К дорогостоящим способам увеличения мощности и крутящего момента двигателя относятся:
Установка наддува на атмосферный двигатель
Это самый дорогостоящий и сложный способ технического тюнинга автомобиля, включающий в себя ряд сложных мероприятий (подбор нагнеталеля, форсирование двигателя, доработка коллекторов, тестирование и т.д. и т.п.). При этом установка наддува может в огромной степени увеличить как мощность, так и крутящий момент за счет значительного увеличения поступаемого в камеру сгорания воздуха. Наддув бывает двух типов: наиболее распространенный турбонаддув (анг. «turbocharger») и механический наддув (компрессор, анг. «supercharger»).
Замена двигателя
Определенно чтобы увеличить мощность и крутящий момент таким способом требуется большой опыт исполнителя и значительные финансовые затраты как на новый мотор, так и на его установку, которая подразумевает под собой ряд мероприятий: определение подходящего двигателя для замены, доработка подкапотного пространства, подключение электрики, замена ЭБУ и прочее.
Форсирование
Подразумевает механическое вмешательство в устройство двигателя: замена определенных его элементов (например, распредвала, дроссельной заслонки или турбины) на спортивные, а так же расточка блока цилиндров, что приведет к увеличению объема мотора и соответственно к увеличению мощности и крутящего момента. Кроме того, двигатель станет намного требовательнее к обслуживанию.
Бюджетные и доступные способы увеличения мощности и крутящего момента
 Так же существуют менее затратные и доступные способы, не подразумевающие технического вмешательства в устройство двигателя. Основным принципом подобных методов является устранение ограничителей в работе двигателя, предусмотренных изготовителем в целях соответствия автомобиля экологическим стандартам, а так же в целях снижения числа гарантийных обращений в сервисные центры.
К доступным способам увеличения мощности относятся:
Так же существуют менее затратные и доступные способы, не подразумевающие технического вмешательства в устройство двигателя. Основным принципом подобных методов является устранение ограничителей в работе двигателя, предусмотренных изготовителем в целях соответствия автомобиля экологическим стандартам, а так же в целях снижения числа гарантийных обращений в сервисные центры.
К доступным способам увеличения мощности относятся:
Чип-тюнинг
Программная оптимизация работы двигателя, подразумевает собой изменение установленных заводом параметров работы ЭБУ различными методами: с помощью электронных модулей или при помощи ручной корректировки («прошивки») программы блока управления. Электронные модули имеют большой ряд преимуществ перед услугой «прошивки» ЭБУ, а негативные отзывы в их сторону, как правило, не подкреплены никакими фактами. При этом новейшие электронные модули ProRacing OBD способны автоматически, автономно и безопасно увеличивать скоростные характеристики автомобилей. Чип-тюнинг — самый действенный из бюджетных способов увеличения мощности и крутящего момента и не требующий никакого технического вмешательства. Кроме того, грамотный чип-тюнинг способствует снижению расхода топлива.
Доработка или замена системы впуска воздуха
Это достигается установкой фильтра нулевого сопротивления либо полной заменой штатной системы впуска. В первом случае прирост мощности будет в пределах 2-5% за счет снижения сопротивления фильтрующего элемента входящему потоку воздуха, во втором же случае увеличение может быть весьма значительным не только за счет снижения сопротивления фильтра, но и за счет увеличения поступления холодного воздуха. Данный способ заслуживает подробного изучения и требует правильного подхода к осуществлению, иначе можно серьезно навредить двигателю либо просто не ощутить результат.
Доработка или замена системы выпуска выхлопных газов
 В угоду экологии, а так же для значительного снижения исходящего шума стандартная система выхлопа в определенной мере ограничивает возможности двигателя. Определенные меры, например, замена катализатора на пламегаситель и удаление антисажевого фильтра, облегчат «выдох» двигателя и обеспечат определенное количество дополнительных лошадиных сил и ньютон-метров. Более дорогим, но и более действенным способом является полная замена штатной выхлопной системы на спортивную. Это даст не только заметную прибавку мощности и крутящему моменту, но и уровняет срок жизни выхлопной системы со сроком жизни автомобиля в целом, т.к. спортивные системы выхлопа изготавливаются из качественной нержавеющей стали.
В угоду экологии, а так же для значительного снижения исходящего шума стандартная система выхлопа в определенной мере ограничивает возможности двигателя. Определенные меры, например, замена катализатора на пламегаситель и удаление антисажевого фильтра, облегчат «выдох» двигателя и обеспечат определенное количество дополнительных лошадиных сил и ньютон-метров. Более дорогим, но и более действенным способом является полная замена штатной выхлопной системы на спортивную. Это даст не только заметную прибавку мощности и крутящему моменту, но и уровняет срок жизни выхлопной системы со сроком жизни автомобиля в целом, т.к. спортивные системы выхлопа изготавливаются из качественной нержавеющей стали.
Использование качественных расходных материалов
Иридиевые свечи зажигания
Данный способ нельзя назвать тюнингом, но это не значит, что им нужно пренебрегать. Использование качественных и дорогих расходных материалов, таких как моторное масло, фильтры, свечи зажигания, а так же топливо, самым непосредственным образом влияют как на мощность, так и на крутящий момент. Отдельным пунктом можно выделить использование дорогих иридиевых или платиновых свечей зажигания, которые очень значительно влияют на работу бензиновых двигателей и способны не только увеличить мощность и крутящий момент, но и снизить расход топлива.
Подписывайтесь на наши ленты в таких социальных сетях как, Facebook, Вконтакте, Instagram, Pinterest, Yandex Zen, Twitter и Telegram: все самые интересные автомобильные события собранные в одном месте.
auto.today
Что такое крутящий момент двигателя автомобиля
Читая характеристики двигателя той или иной модели, мы встречаем такие понятия:
- мощность — лошадиные силы;
- максимальный крутящий момент — Ньютон/метры;
- обороты в минуту.
Люди, увидев значение 100 или 200 лошадиных сил, полагают, что это очень хорошо. И они правы — 200 лошадиных сил для мощного кроссовера или 100 л.с. для компактного городского хетчбэка действительно неплохие показатели. Но нужно обращать внимание также на максимальный крутящий момент и обороты двигателя, поскольку такая мощность достигается на пике работы двигателя.
Говоря простым языком, максимальную мощность в 100 л.с. ваш двигатель может развить при определенных оборотах двигателя. Если же вы ездите по городу, а стрелка тахометра показывает 2000-2500 оборотов, тогда как максимум составляет 4-5-6 тысяч, то в данный момент используется лишь часть этой мощности — 50 или 60 лошадиных сил. Соответственно и скорость будет небольшая.
Если же вам нужно перейти на более быстрый режим движения — выехали на скоростную трассу или хотите обогнать фуру — вам нужно увеличить количество оборотов, тем самым увеличив скорость.
Момент силы, он же крутящий момент, как раз и определяет, как быстро ваша машина может ускориться и выдать максимум мощности.
Другой пример — вы едете по трассе, на большой скорости на 4-5 передаче. Если же дорога начинает подниматься в гору и уклон довольно ощутимый, то мощности двигателя может просто не хватить. Поэтому приходится переключаться на пониженные передачи, при этом выжимая большую мощность с двигателя. Крутящий момент в данном случае служит для увеличения мощности и помогает активизировать все силы вашего двигателя на преодоление препятствия.
Наибольший крутящий момент выдают бензиновые двигатели — при 3500-6000 оборотов в минуту в зависимости от марки автомобиля. У дизельных моторов максимальный крутящий момент наблюдается при 3-4 тысячах оборотов. Соответственно, у дизельных автомобилей динамика разгона лучше, им проще быстро разгоняться и выжимать всех «лошадей» с мотора.
Однако, по максимальной мощности они проигрывают своим бензиновым собратьям, поскольку при 6000 оборотах мощность у бензинового автомобиля может достигать нескольких сотен лошадиных сил. Не зря ведь все самые быстрые и мощные автомобили, о которых мы писали на Vodi.su ранее, работают исключительно на высокооктановом бензине А-110.
Ну и чтоб стало совсем понятно, что такое крутящий момент, нужно посмотреть на единицы его измерения: Ньютоны на метры. Говоря простым языком, это сила с которой мощность передается от поршня через шатуны и коленчатый вал на маховик. А уже от маховика эта сила передается на трансмиссию — коробку передач и от нее на колеса. Чем быстрее движется поршень, тем быстрее вращается маховик.
Отсюда приходим к выводу, что мощность двигателя производит крутящий момент. Есть техника, в которой максимальная тяга вырабатывается на низких оборотах — 1500-2000 об/мин. Действительно, в тракторах, самосвалах или внедорожниках мы прежде всего ценим мощность — водителю джипа некогда раскручивать коленвал до 6-ти тысяч оборотов, чтобы выехать из ямы. То же самое можно сказать о тракторе, который тянет тяжелую дисковую борону или трехкорпусный плуг — максимальная мощность нужна ему на малых оборотах.
От чего зависит крутящий момент
Понятно, что самые мощные моторы обладают самым большим объемом. Если у вас какая-нибудь малолитражка типа Daewoo Nexia 1.5L или компактный хетчбэк Hyundai i10 1.1L, то резко разогнаться или стартовать с места с пробуксовкой вряд ли получится, хотя умение правильно переключать передачи и использовать всю мощь мотора делает свое дело.
Соответственно, на малолитражках мы используем лишь часть потенциала двигателя, тогда как на более мощных автомобилях с хорошими показателями и эластичностью двигателя — диапазонами переключения передач — можно разгоняться практически с места, при этом не переключая передачи так быстро.
Эластичность двигателя — это важный параметр, говорящий о том, что соотношение мощности и количества оборотов оптимальное. Можно ехать на пониженных передачах с довольно большой скоростью, выжимая при этом максимум с двигателя. Это очень хорошее качество как для городского режима езды, где нужно постоянно тормозить, разгоняться и снова останавливаться, — так и для трассы — одним нажатием на педаль можно разогнать двигатель до высоких оборотов.
Крутящий момент — один из самых важных параметров двигателя
Таким образом мы приходим к выводу, что все параметры двигателя тесно связаны между собой: мощность, крутящий момент, количество оборотов в минуту, при которых достигается максимальный крутящий момент.
Крутящий момент является той силой, которая помогает полностью использовать всю мощь двигателя. Ну а чем больше мощность мотора, тем больше крутящий момент. Если же он еще и достигается на невысоких оборотах, то на такой машине можно будет легко разогнаться с места, или взобраться на любую горку, не переходя на пониженные передачи.
На этом видео прекрасно разобрали что такое крутящий момент и лошадиные силы.
Загрузка…Поделиться в социальных сетях
vodi.su
Крутящий момент — это… Что такое Крутящий момент?
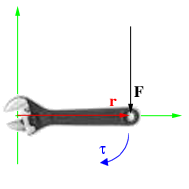
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.
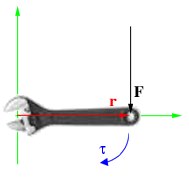
Момент силы приложенный к гаечному ключу
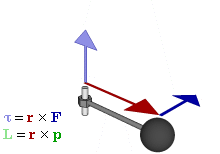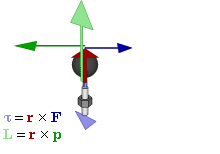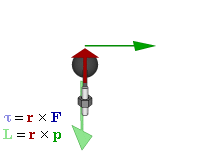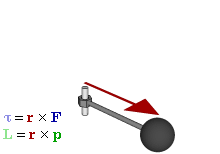
Отношение между векторами силы, момента силы и импульса во вращающейся системе
Момент силы
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:
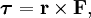
где 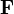 — сила, действующая на частицу, а
— сила, действующая на частицу, а 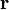 — радиус-вектор частицы!
— радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы 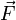 на рычаг
на рычаг 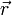 , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
, совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок 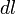 , которому соответствует бесконечно малый угол
, которому соответствует бесконечно малый угол 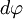 . Обозначим через
. Обозначим через 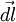 вектор, который направлен вдоль бесконечно малого отрезка
вектор, который направлен вдоль бесконечно малого отрезка 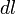 и равен ему по модулю. Угол между вектором силы
и равен ему по модулю. Угол между вектором силы 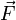 и вектором
и вектором 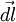 равен
равен 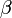 , а угол
, а угол 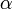
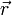 и вектором силы
и вектором силы 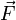 .
.
Следовательно, бесконечно малая работа 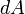 , совершаемая силой
, совершаемая силой 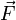 на бесконечно малом участке
на бесконечно малом участке 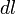 равна скалярному произведению вектора
равна скалярному произведению вектора 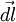 и вектора силы, то есть
и вектора силы, то есть 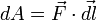 .
.
Теперь попытаемся выразить модуль вектора 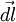 через радиус вектор
через радиус вектор 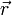 , а проекцию вектора силы
, а проекцию вектора силы 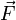 на вектор
на вектор 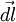 , через угол
, через угол 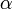 .
.
В первом случае, используя теорему Пифагора, можно записать следующее равенство 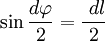 , где в случае малого угла справедливо
, где в случае малого угла справедливо 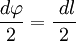 и следовательно
и следовательно 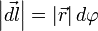
Для проекции вектора силы 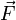 на вектор
на вектор 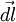 , видно, что угол
, видно, что угол 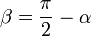 , так как для бесконечно малого перемещения рычага
, так как для бесконечно малого перемещения рычага 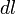 , можно считать, что траектория перемещения перпендикулярна рычагу
, можно считать, что траектория перемещения перпендикулярна рычагу 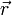 , а так как
, а так как 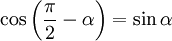 , получаем, что
, получаем, что 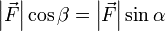 .
.
Теперь запишем бесконечно малую работу через новые равенства 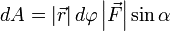 или
или 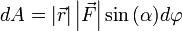 .
.
Теперь видно, что произведение 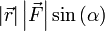 есть ни что иное как модуль векторного произведения векторов
есть ни что иное как модуль векторного произведения векторов 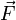 и
и 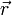 , то есть
, то есть 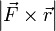 , которое и было принято обозначить за момент силы
, которое и было принято обозначить за момент силы 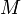 или модуля вектора момента силы
или модуля вектора момента силы 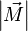 .
.
И теперь полная работа записывается очень просто 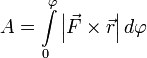 или
или 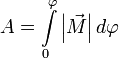 .
.
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
 ,
,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
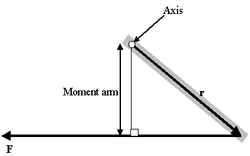
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
 = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
= РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
 ,
,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
 ,
,
То есть если I постоянная, то
 ,
,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
 = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
= МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность 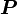 измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
 = МОМЕНТ СИЛЫ * УГОЛ
= МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа 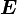 измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
Обычно известна угловая скорость 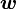 в радианах в секунду и время действия МОМЕНТА
в радианах в секунду и время действия МОМЕНТА 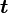 .
.
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
 = МОМЕНТ СИЛЫ *
= МОМЕНТ СИЛЫ *  *
* 
Момент силы относительно точки
Если имеется материальная точка 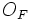 , к которой приложена сила
, к которой приложена сила 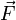 , то момент силы относительно точки
, то момент силы относительно точки 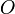 равен векторному произведению радиус-вектора
равен векторному произведению радиус-вектора 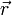 , соединяющий точки O и OF, на вектор силы
, соединяющий точки O и OF, на вектор силы 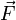 :
:
![\vec M_O = \left[ \vec r \times \vec F \right]](/800/600/https/biograf.academic.ru/pictures/wiki/files/48/060f481774ea2ae7875fb856dd7d28d8.png) .
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
Wikimedia Foundation. 2010.
biograf.academic.ru
Крутящий момент — это… Что такое Крутящий момент?
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.

Момент силы приложенный к гаечному ключу

Отношение между векторами силы, момента силы и импульса во вращающейся системе
Момент силы
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:
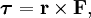
где 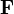 — сила, действующая на частицу, а
— сила, действующая на частицу, а 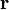 — радиус-вектор частицы!
— радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы 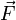 на рычаг
на рычаг 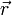 , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
, совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок 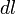 , которому соответствует бесконечно малый угол
, которому соответствует бесконечно малый угол 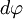 . Обозначим через
. Обозначим через 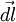 вектор, который направлен вдоль бесконечно малого отрезка
вектор, который направлен вдоль бесконечно малого отрезка 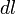 и равен ему по модулю. Угол между вектором силы
и равен ему по модулю. Угол между вектором силы 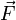 и вектором
и вектором 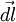 равен
равен 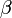 , а угол
, а угол 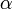
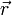 и вектором силы
и вектором силы 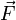 .
.
Следовательно, бесконечно малая работа 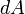 , совершаемая силой
, совершаемая силой 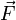 на бесконечно малом участке
на бесконечно малом участке 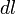 равна скалярному произведению вектора
равна скалярному произведению вектора 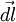 и вектора силы, то есть
и вектора силы, то есть 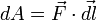 .
.
Теперь попытаемся выразить модуль вектора 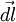 через радиус вектор
через радиус вектор 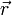 , а проекцию вектора силы
, а проекцию вектора силы 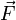 на вектор
на вектор 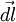 , через угол
, через угол 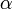 .
.
В первом случае, используя теорему Пифагора, можно записать следующее равенство 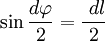 , где в случае малого угла справедливо
, где в случае малого угла справедливо 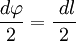 и следовательно
и следовательно 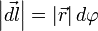
Для проекции вектора силы 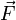 на вектор
на вектор 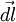 , видно, что угол
, видно, что угол 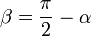 , так как для бесконечно малого перемещения рычага
, так как для бесконечно малого перемещения рычага 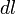 , можно считать, что траектория перемещения перпендикулярна рычагу
, можно считать, что траектория перемещения перпендикулярна рычагу 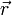 , а так как
, а так как 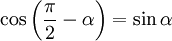 , получаем, что
, получаем, что 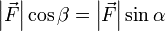 .
.
Теперь запишем бесконечно малую работу через новые равенства 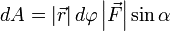 или
или 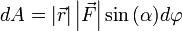 .
.
Теперь видно, что произведение 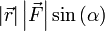 есть ни что иное как модуль векторного произведения векторов
есть ни что иное как модуль векторного произведения векторов 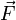 и
и 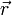 , то есть
, то есть 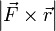 , которое и было принято обозначить за момент силы
, которое и было принято обозначить за момент силы 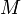 или модуля вектора момента силы
или модуля вектора момента силы 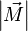 .
.
И теперь полная работа записывается очень просто 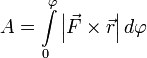 или
или 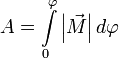 .
.
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
 ,
,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага

Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
 = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
= РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
 ,
,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
 ,
,
То есть если I постоянная, то
 ,
,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
 = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
= МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность 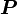 измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
 = МОМЕНТ СИЛЫ * УГОЛ
= МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа 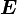 измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
Обычно известна угловая скорость 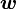 в радианах в секунду и время действия МОМЕНТА
в радианах в секунду и время действия МОМЕНТА 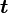 .
.
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
 = МОМЕНТ СИЛЫ *
= МОМЕНТ СИЛЫ *  *
* 
Момент силы относительно точки
Если имеется материальная точка 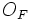 , к которой приложена сила
, к которой приложена сила 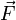 , то момент силы относительно точки
, то момент силы относительно точки 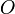 равен векторному произведению радиус-вектора
равен векторному произведению радиус-вектора 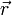 , соединяющий точки O и OF, на вектор силы
, соединяющий точки O и OF, на вектор силы 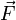 :
:
![\vec M_O = \left[ \vec r \times \vec F \right]](/800/600/https/biograf.academic.ru/pictures/wiki/files/48/060f481774ea2ae7875fb856dd7d28d8.png) .
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
Wikimedia Foundation. 2010.
biograf.academic.ru
Крутящий момент — это… Что такое Крутящий момент?
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.
Момент силы приложенный к гаечному ключу
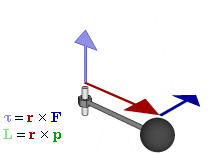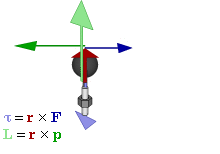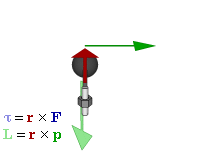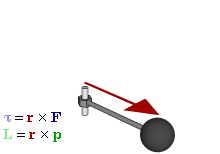
Отношение между векторами силы, момента силы и импульса во вращающейся системе
Момент силы
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:
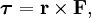
где 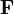 — сила, действующая на частицу, а
— сила, действующая на частицу, а 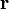 — радиус-вектор частицы!
— радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы 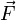 на рычаг
на рычаг 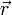 , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
, совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок 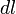 , которому соответствует бесконечно малый угол
, которому соответствует бесконечно малый угол 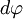 . Обозначим через
. Обозначим через 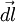 вектор, который направлен вдоль бесконечно малого отрезка
вектор, который направлен вдоль бесконечно малого отрезка 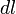 и равен ему по модулю. Угол между вектором силы
и равен ему по модулю. Угол между вектором силы 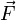 и вектором
и вектором 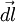 равен
равен 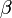 , а угол
, а угол 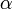
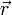 и вектором силы
и вектором силы 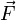 .
.
Следовательно, бесконечно малая работа 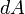 , совершаемая силой
, совершаемая силой 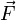 на бесконечно малом участке
на бесконечно малом участке 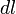 равна скалярному произведению вектора
равна скалярному произведению вектора 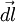 и вектора силы, то есть
и вектора силы, то есть 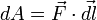 .
.
Теперь попытаемся выразить модуль вектора 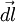 через радиус вектор
через радиус вектор 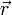 , а проекцию вектора силы
, а проекцию вектора силы 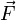 на вектор
на вектор 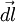 , через угол
, через угол 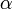 .
.
В первом случае, используя теорему Пифагора, можно записать следующее равенство 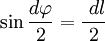 , где в случае малого угла справедливо
, где в случае малого угла справедливо 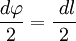 и следовательно
и следовательно 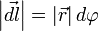
Для проекции вектора силы 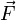 на вектор
на вектор 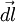 , видно, что угол
, видно, что угол 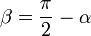 , так как для бесконечно малого перемещения рычага
, так как для бесконечно малого перемещения рычага 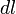 , можно считать, что траектория перемещения перпендикулярна рычагу
, можно считать, что траектория перемещения перпендикулярна рычагу 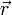 , а так как
, а так как 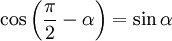 , получаем, что
, получаем, что 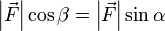 .
.
Теперь запишем бесконечно малую работу через новые равенства 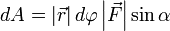 или
или 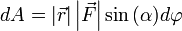 .
.
Теперь видно, что произведение 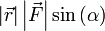 есть ни что иное как модуль векторного произведения векторов
есть ни что иное как модуль векторного произведения векторов 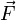 и
и 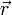 , то есть
, то есть 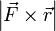 , которое и было принято обозначить за момент силы
, которое и было принято обозначить за момент силы 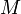 или модуля вектора момента силы
или модуля вектора момента силы 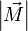 .
.
И теперь полная работа записывается очень просто 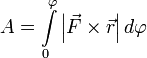 или
или 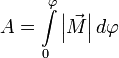 .
.
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
 ,
,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
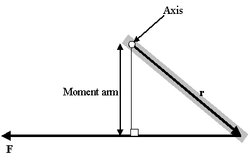
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
 = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
= РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
 ,
,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
 ,
,
То есть если I постоянная, то
 ,
,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
 = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
= МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность 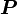 измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
 = МОМЕНТ СИЛЫ * УГОЛ
= МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа 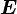 измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
Обычно известна угловая скорость 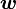 в радианах в секунду и время действия МОМЕНТА
в радианах в секунду и время действия МОМЕНТА 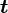 .
.
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
 = МОМЕНТ СИЛЫ *
= МОМЕНТ СИЛЫ *  *
* 
Момент силы относительно точки
Если имеется материальная точка 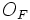 , к которой приложена сила
, к которой приложена сила 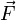 , то момент силы относительно точки
, то момент силы относительно точки 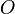 равен векторному произведению радиус-вектора
равен векторному произведению радиус-вектора 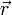 , соединяющий точки O и OF, на вектор силы
, соединяющий точки O и OF, на вектор силы 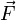 :
:
![\vec M_O = \left[ \vec r \times \vec F \right]](/800/600/https/dal.academic.ru/pictures/wiki/files/48/060f481774ea2ae7875fb856dd7d28d8.png) .
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
Wikimedia Foundation. 2010.
dal.academic.ru

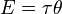 ,
,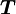 = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
= РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ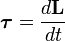 ,
,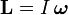 ,
,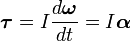 ,
,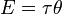 ,
,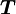 = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
= РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ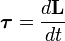 ,
,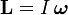 ,
,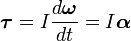 ,
,