Как определить крутящий момент – Как определить крутящий момент 🚩 как рассчитать крутящий момент электродвигателя 🚩 Естественные науки

Момент силы — Википедия

Момент силы, приложенный к гаечному ключу. Направлен от зрителя

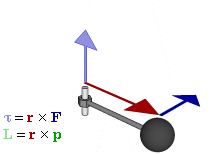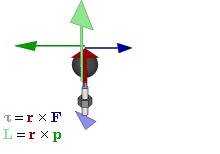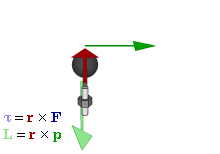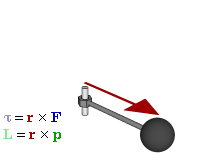
Моме́нт си́лы (синонимы: кру́тящий момент, враща́тельный момент, вертя́щий момент, враща́ющий момент) — векторная физическая величина, равная векторному произведению радиус-вектора, проведённого от оси вращения к точке приложения силы и вектора этой силы. Характеризует вращательное действие силы на твёрдое тело.

Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов).

В физике момент силы можно понимать как «вращающая сила». В Международной системе единиц (СИ) единицей измерения момента силы является ньютон-метр (Н·м). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метра от его оси вращения, создаёт такой же момент, что и сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров от оси вращения. Более точно момент силы частицы определяется как векторное произведение:

M→=[r→×F→],{\displaystyle {\vec {M}}=\left[{\vec {r}}\times {\vec {F}}\right],}

где F→{\displaystyle {\vec {F}}} — сила, действующая на частицу, а r→{\displaystyle {\vec {r}}} — радиус-вектор частицы (в предположении, что ось вращения проходит через начало координат).

Для того чтобы понять, откуда появилось обозначение момента сил и как к нему пришли, стоит рассмотреть действие силы на рычаг, поворачивающийся относительно неподвижной оси. Работа, совершаемая при действии силы F→{\displaystyle {\vec {F}}} на рычаг r→{\displaystyle {\vec {r}}}, совершающий вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.

Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок dl{\displaystyle dl}, которому соответствует бесконечно малый угол dφ{\displaystyle d\varphi }. Обозначим через d→l{\displaystyle {\vec {d}}l} вектор, который направлен вдоль бесконечно малого отрезка dl{\displaystyle dl} и равен ему по модулю. Угол между вектором силы F→{\displaystyle {\vec {F}}} и вектором d→l{\displaystyle {\vec {d}}l} равен β{\displaystyle \beta }, а угол между векторами r→{\displaystyle {\vec {r}}} и F→{\displaystyle {\vec {F}}} — α{\displaystyle \alpha }.

Следовательно, бесконечно малая работа dA{\displaystyle dA}, совершаемая силой F→{\displaystyle {\vec {F}}} на бесконечно малом участке dl{\displaystyle dl}, равна скалярному произведению вектора d→l{\displaystyle {\vec {d}}l} и вектора силы, то есть dA=F→⋅d→l{\displaystyle dA={\vec {F}}\cdot {\vec {d}}l}.

Теперь попытаемся выразить модуль вектора d→l{\displaystyle {\vec {d}}l} через радиус-вектор r→{\displaystyle {\vec {r}}}, а проекцию вектора силы F→{\displaystyle {\vec {F}}} на вектор d→l{\displaystyle {\vec {d}}l} — через угол α{\displaystyle \alpha }.

Так как для бесконечно малого перемещения рычага dl{\displaystyle dl} можно считать, что траектория перемещения перпендикулярна рычагу r→{\displaystyle {\vec {r}}}, используя соотношения для прямоугольного треугольника, можно записать следующее равенство: dl=rtgdφ{\displaystyle dl=r\mathrm {tg} \,d\varphi }, где в случае малого угла справедливо tgdφ=dφ{\displaystyle \mathrm {tg} \,d\varphi =d\varphi } и, следовательно, |dl→|=|r→|dφ{\displaystyle \left|{\vec {dl}}\right|=\left|{\vec {r}}\right|d\varphi }.

Для проекции вектора силы F→{\displaystyle {\vec {F}}} на вектор d→l{\displaystyle {\vec {d}}l} видно, что угол β=π2−α{\displaystyle \beta ={\frac {\pi }{2}}-\alpha }, а так как cos⁡(π2−α)=sin⁡α{\displaystyle \cos {\left({\frac {\pi }{2}}-\alpha \right)}=\sin \alpha }, получаем, что |F→|cos⁡β=|F→|sin⁡α{\displaystyle \left|{\vec {F}}\right|\cos \beta =\left|{\vec {F}}\right|\sin \alpha }.

Теперь запишем бесконечно малую работу через новые равенства: dA=|r→|dφ|F→|sin⁡α{\displaystyle dA=\left|{\vec {r}}\right|d\varphi \left|{\vec {F}}\right|\sin \alpha }, или dA=|r→||F→|sin⁡(α)dφ{\displaystyle dA=\left|{\vec {r}}\right|\left|{\vec {F}}\right|\sin(\alpha )d\varphi }.

Теперь видно, что произведение |r→||F→|sin⁡α{\displaystyle \left|{\vec {r}}\right|\left|{\vec {F}}\right|\sin \alpha } есть не что иное, как модуль векторного произведения векторов r→{\displaystyle {\vec {r}}} и F→{\displaystyle {\vec {F}}}, то есть |r→×F→|{\displaystyle \left|{\vec {r}}\times {\vec {F}}\right|}, которое и было принято обозначить за момент силы M{\displaystyle M}, или модуль вектора момента силы |M→|{\displaystyle \left|{\vec {M}}\right|}.

Теперь полная работа записывается просто: A=∫0φ|r→×F→|dφ{\displaystyle A=\int \limits _{0}^{\varphi }\left|{\vec {r}}\times {\vec {F}}\right|d\varphi }, или A=∫0φ|M→|dφ{\displaystyle A=\int \limits _{0}^{\varphi }\left|{\vec {M}}\right|d\varphi }.

Момент силы имеет размерность «сила, умноженная на расстояние» и единицу измерения ньютон-метр в системе СИ. 1 Н·м — это момент, который производит сила 1 Н на рычаг длиной 1 м, приложенная к концу рычага и направленная перпендикулярно ему.

Энергия и механическая работа также имеют размерность «сила, умноженная на расстояние» и измеряются в системе СИ в джоулях. Следует заметить, что энергия — это скалярная величина, тогда как момент силы — величина псевдовекторная. Совпадение размерностей этих величин не случайность: момент силы 1 Н·м, при повороте рычага или вала на 1 радиан совершает работу в 1 Дж, а при повороте на один оборот совершает механическую работу и сообщает энергию 2π{\displaystyle 2\pi } джоуля. Математически:

E=Mθ,{\displaystyle E=M\theta ,}

где E{\displaystyle E} — энергия, M{\displaystyle M} — вращающий момент, θ{\displaystyle \theta } — угол в радианах.

Формула момента рычага[править | править код]

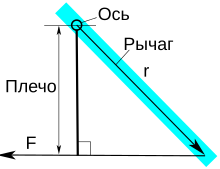Момент, действующий на рычаг

Очень интересен особый случай, представляемый как определение момента силы в поле:

|M→|=|M→1||F→|,{\displaystyle \left|{\vec {M}}\right|=\left|{\vec {M}}_{1}\right|\left|{\vec {F}}\right|,}

где: |M→1|{\displaystyle \left|{\vec {M}}_{1}\right|} — момент рычага, |F→|{\displaystyle \left|{\vec {F}}\right|} — величина действующей силы.

Недостаток такого представления в том, что оно не дает направления момента силы, а только его величину. Если сила перпендикулярна вектору r→{\displaystyle {\vec {r}}}, момент рычага будет равен расстоянию от центра до точки приложения силы и момент силы будет максимален:

|T→|=|r→||F→|.{\displaystyle \left|{\vec {T}}\right|=\left|{\vec {r}}\right|\left|{\vec {F}}\right|.}

Сила под углом[править | править код]

Если сила F→{\displaystyle {\vec {F}}} направлена под углом θ{\displaystyle \theta } к рычагу r, то M=rFsin⁡θ{\displaystyle M=rF\sin \theta }.

Статическое равновесие[править | править код]

Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для двумерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0,ΣV=0{\displaystyle \Sigma H=0,\,\Sigma V=0} и момент силы в третьем измерении ΣM=0{\displaystyle \Sigma M=0}.

Момент силы как функция от времени[править | править код]

Момент силы — производная по времени от момента импульса,

Видеоурок: вращающий момент

M→=dL→dt,{\displaystyle {\vec {M}}={\frac {d{\vec {L}}}{dt}},}

где L→{\displaystyle {\vec {L}}} — момент импульса.

Возьмём твердое тело. Движение твёрдого тела можно представить как движение конкретной точки и вращения вокруг неё.

Момент импульса относительно точки O твёрдого тела может быть описан через произведение момента инерции и угловой скорости относительно центра масс и линейного движения центра масс.

Lo→=Icω→+[M(ro→−rc→),vc→].{\displaystyle {\vec {L_{o}}}=I_{c}\,{\vec {\omega }}+[M({\vec {r_{o}}}-{\vec {r_{c}}}),{\vec {v_{c}}}].}

Будем рассматривать вращающиеся движения в системе координат Кёнига, так как описывать движение твёрдого тела в мировой системе координат гораздо сложнее.

Продифференцируем это выражение по времени. И если I{\displaystyle I} — постоянная величина во времени, то

M→=Idω→dt=Iα→,{\displaystyle {\vec {M}}=I{\frac {d{\vec {\omega }}}{dt}}=I{\vec {\alpha }},}

где α→{\displaystyle {\vec {\alpha }}} — угловое ускорение, измеряемое в радианах в секунду за секунду (рад/с²). Пример: вращается однородный диск.

Если тензор инерции меняется со временем, то движение относительно центра масс описывается с помощью динамического уравнения Эйлера:

Mc→=Icdω→dt+[w→,Icw→].{\displaystyle {\vec {M_{c}}}=I_{c}{\frac {d{\vec {\omega }}}{dt}}+[{\vec {w}},I_{c}{\vec {w}}].}

Отношение между моментом силы и мощностью[править | править код]

Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Так же и момент силы, если совершает действие через угловое расстояние, он совершает работу.

P=M→⋅ω→.{\displaystyle P={\vec {M}}\cdot {\vec {\omega }}.}

В системе СИ мощность P{\displaystyle P} измеряется в ваттах, момент силы — в ньютоно-метрах, а угловая скорость — в радианах в секунду.

Отношение между моментом силы и работой[править | править код]

A=∫θ1θ2|M→|dθ.{\displaystyle A=\int _{\theta _{1}}^{\theta _{2}}\left|{\vec {M}}\right|\mathrm {d} \theta .}

В случае постоянного момента получаем:

A=|M→|θ.{\displaystyle A=\left|{\vec {M}}\right|\theta .}

В системе СИ работа A{\displaystyle A} измеряется в джоулях, момент силы — в ньютоно-метрах, а угол — в радианах.

Обычно известна угловая скорость ω{\displaystyle \omega } в радианах в секунду и время действия момента t{\displaystyle t}.

Тогда совершённая моментом силы работа рассчитывается как:

A=|M→|ωt.{\displaystyle A=\left|{\vec {M}}\right|\omega t.}

Если имеется материальная точка OF{\displaystyle O_{F}}, к которой приложена сила F→{\displaystyle {\vec {F}}}, то момент силы относительно точки O{\displaystyle O} равен векторному произведению радиус-вектора r→{\displaystyle {\vec {r}}}, соединяющего точки O{\displaystyle O} и OF{\displaystyle O_{F}}, на вектор силы F→{\displaystyle {\vec {F}}}:

MO→=[r→×F→].{\displaystyle {\vec {M_{O}}}=\left[{\vec {r}}\times {\vec {F}}\right].}

Момент силы относительно оси равен алгебраическому значению проекции момента этой силы на плоскость, перпендикулярную этой оси относительно точки пересечения оси с плоскостью, то есть

Mz(F)=Mo(F′)=F′h′.{\displaystyle M_{z}(F)=M_{o}(F’)=F’h’.}

Измерение момента силы осуществляется с помощью специальных приборов — торсиометров. Принцип их действия обычно основан на измерении угла закручивания упругого вала, передающего крутящий момент, либо на измерении деформации некоторого упругого рычага. Измерения деформации и угла закручивания производится различными датчиками деформации — тензометрическими, магнитоупругими, а также измерителями малых перемещений — оптическими, ёмкостными,

что такое, формула и в чем измеряется

Мощность двигателя – важнейший его показатель. Как в плане эксплуатации, так и в плане начисления налогов на авто. Крутящий момент нередко путают с мощностью или упускают его из виду в процессе оценки ходовых качеств авто. Многие упрощают автомобиль, считая, что большое количество лошадиных сил – главное преимущество любого мотора. Однако, вращающий момент – более важный показатель. Особенно, если автомобиль не предполагается использовать в качестве спортивного.

Что такое крутящий момент

Крутящим моментом называют единицу силы, которая необходима для поворота коленчатого вала ДВС. Эта не «лошадиная сила», которой должна обозначаться мощность.

ДВС вырабатывает кинетическую энергию, вращая таким образом коленвал. Показатель мощности двигателя (сила давления) зависит от скорости сгорания топлива. Крутящий момент – результат от действия силы на рычаг. Эта сила в физике считается в ньютонах. Длина плеча коленвала считается в метрах. Поэтому обозначение крутящего момента – ньютон-метр.

Технически, крутящий момент – это усилие, которое должно осуществляться двигателем для разгона и движения машины. При этом сила, оказывающая действие на поршень, пропорциональна объему двигателя.

Маховик – одна из важнейших деталей, которая должна через редуктор передавать вращательный момент от мотора к коробке передач, от стартера на коленвал, от коленвала на нажимной диск. Собственно, крутящий момент – итог давления на шатун.

Формула расчета крутящего момента

Показатель КМ рассчитывается так: мощность (в л. с.) равно крутящий момент (в Нм) умножить на обороты в минуту и разделить на 5,252. При меньших чем 5,252 значениях крутящий момент будет выше мощности, при больших – ниже.

В пересчете на принятую в России систему (кгм – килограмм на метр) – 1кг = 10Н, 1 см = 0,01м. Таким образом 1 кг х см = 0,1 Н х м. Посчитать вращательный момент в разных системах измерений ньютоны/килограммы и т.д. поможет конвертер – в практически неизменном виде он доступен на множестве сайтов, с его помощью можно определять данные по практически любому мотору.

График:

На графике изображена зависимость крутящего момента двигателя от его оборотов

От чего зависит крутящий момент

На КМ будут влиять:

• Объем двигателя.
• Давление в цилиндрах.
• Площадь поршней.
• Радиус кривошипа коленвала.

Основная механика образования КМ заключается в том, что чем больше двигатель по объему, тем сильней он будет нагружать поршень. То есть – будет выше значение КМ. Аналогична взаимосвязь с радиусом кривошипа коленвала, но это вторично: в современных двигателях этот радиус сильно изменить нельзя.

Давление в камере сгорания – не менее важный фактор. От него напрямую зависит сила, давящая на поршень.

Для снижения потерь крутящего момента при тряске машины во время резкого газа можно использовать компенсатор. Это специальный (собранный вручную) демпфер, компенсация которого позволит сохранить вращающий момент и повысить срок эксплуатации деталей.

На что влияет крутящий момент

Главная цель КМ – набор мощности. Часто мощные моторы обладают низким показателем КМ, поэтому не способны разогнать машину достаточно быстро. Особенно это касается бензиновых двигателей.

ВАЖНО! При выборе авто стоит рассчитать оптимальное соотношение вращательного момента с количеством оборотов, на которых чаще всего мотор будет работать. Если держать вращательный момент на соответствующем уровне, это позволит оптимально реализовать потенциал двигателя.

Высокий КМ также может влиять на управляемость машины, поэтому при резком увеличении скорости не лишним будет использование системы TSC. Она позволяет точнее направлять авто при резком разгоне.

Широко распространенный 8-клапанный двигатель ВАЗ выдает вращательный момент 120 (при 2500-2700 оборотах). Ручная коробка или АКПП стоит на машине – не принципиально. При использовании КПП немаловажен опыт водителя, на автоматической коробке плавный старт обеспечивает преобразователь.

Как увеличить крутящий момент

Увеличение рабочего объема. Чтобы повышать КМ используются разные методы: замена установленного коленвала на вал с увеличенным эксцентриситетом (редко встречающаяся запчасть, которую трудно находить) или расточка цилиндров под больший диаметр поршней. Оба способа имеют свои плюсы и минусы. Первый требует много времени на подбор деталей и снижает долговечность двигателя. Второй, увеличение диаметра цилиндров с помощью расточки, более популярен. Это может сделать практически любой автосервис. Там же можно настроить карбюратор для повышения КМ.

Изменение величины наддува. Турбированные двигатели позволяют достичь более высокого показателя КМ благодаря особенностям конструкции – возможности отключить ограничения в блоке управления компрессором, который отвечает за наддув. Манипуляции с блоком позволят повысить объем давления выше максимума, указанного производителем при сборке автомобиля. Способ можно назвать опасным, поскольку у каждого двигателя есть лимитированный запас нагрузок. Кроме того, часто требуются дополнительные усовершенствования: увеличение камеры сгорания, приведение охлаждения в соответствие повышенной мощности. Иногда требуется отрегулировать впускной клапан, иногда – сменить распредвал. Может потребоваться замена чугунного коленвала на стальной, замена поршней.

Изменение газодинамики. Редко используемый вариант, поскольку двигатель – сложная конструкция, созданием которого занимаются профессионалы. Теоретически можно придумать, как убрать ограничения, заложенные конструкторами для увеличения срока эксплуатации двигателя и его деталей. Но на практике, если убрать ограничитель, результат не гарантирован, поскольку поменяются все характеристики: например, динамика вырастет, но шина не будет цепляться за дорогу. Чтобы усовершенствовать двигатель такие образом надо быть не просто автомобильным конструктором, но и математиком, физиком и т.д.

ВАЖНО! Простой способ повысить КМ – использовать масляный фильтр. Он снизит засорение двигателя и продлит срок эксплуатации всех деталей.

Определение крутящего момента на валу

Для измерения крутящего момента на валу автомобильного двигателя применяется множество методик. Это может быть показатель подачи топлива, температуры выхлопных газов и т.д. Такие методы не гарантируют высокой точности.

Распространенный метод повышенной точности – применение тензометрического моста. На вал крепятся тензометры, электрически соединенные по мостовой схеме. Сигнал передается на считывающее устройство.

Измеритель крутящего момента

Главная сложность в измерителе крутящего момента, использующего тензометры, является точность передачи данных. Применявшиеся ранее контактные, индукционные и светотехнические устройства не гарантировали необходимой эффективности. Сейчас данные передаются по цифровым радиоканалам. Измеритель представляет собой компактный радиопередатчик, который крепится на вал и передает данные на приемник.

Сейчас такие устройства доступны по стоимости и просты в эксплуатации. Применяются в основном в СТО.

Датчик крутящего момента

Аналогичные устройства, измеряющие КМ, в автомобиле могут быть установлены не только на коленвал, но и на рулевое колесо. Он ставится на модели машин с электроусилителем руля и позволяет отслеживать работу системы управление автомобилей. При выходе датчика из строя, усилитель, как правило, отключается.

Максимальный крутящий момент

Максимальным называется крутящий момент, представляющий пик, после которого момент не растет, несмотря на количество оборотов. На малых оборотах в цилиндре скапливается большой объем остаточных газов, в результате чего показатель КМ значительно ниже пикового. На средних оборотах в цилиндры поступает больше воздуха, процент газов снижается, крутящий момент продолжает расти.

При высоких оборотах растут потери эффективности: от трения поршней, инерционных потерь в ГРМ, разогрева масла и т.д. будет зависеть работа мотора. Поэтому рост качества работы двигателя прекращается или само качество начинает снижаться. Максимальный крутящий момент достигнут и начинает снижаться.

В электродвигателях максимальный вращательный момент называется «критический».

Таблица марок автомобилей с указанием крутящего момента:

Модели автомобиля ВАЗ	Крутящий момент (Нм, разные марки двигателей)
2107	93 – 176
2108	79-186
2109	78-118
2110	104-196
2112	104-162
2114	115-145
2121 (Нива)	116-129
2115	103-132
2106	92-116
2101	85-92
2105	85-186
Двигатели ЗМЗ
406	181,5-230
409	230
Других популярные в России марки автомобилей
Ауди А6	500-750
БМВ 5	290-760
Бугатти Вейрон	1250-1500
Дэу Нексия	123-150
КАМАЗ	~650-2000+
Киа Рио	132-151
Лада Калина	127-148
Мазда 6	165-420
Мицубиси Лансер	143-343
УАЗ Патриот	217-235
Рено Логан	112-152
Рено Дастер	156-240
Тойота Королла	128-173
Хендай Акцент	106-235
Хендай Солярис	132-151
Шевроле Каптив	220-400
Шевроле Круз	118-200

Какому двигателю отдать предпочтение

Сегодня множество моделей производители оснащают разными типами моторов: бензиновым или дизельным. Эти модели идентичны только по цене и другим характеристикам.

Из-за разных типов мотора одна и та же модель может отличаться по показателям мощности мотора и крутящему моменту, при этом разница может быть значительной.

Бензиновый двигатель

Бензиновый двигатель формирует воздушно-топливную смесь, заполняющую цилиндр. Температура внутри него поднимается до примерно 500 градусов. У таких моторов номинальный коэффициент сжатия составляет порядка 9-10, реже 11 единиц. Поэтому, когда происходит впрыск необходимо использование свечей зажигания.

Дизельный двигатель

В цилиндрах работающего на дизеле движка коэффициент сжатия смеси может достигать показателя в 25 единиц, температура – 900 градусов. Поэтому смесь зажигается без использования свечи.

Электродвигатель

Автомобильный трехфазный асинхронный электродвигатель работает по совершенно другим законам, поэтому его мощность и КМ отличаются от традиционных кардинально. Электромотор состоит из ротора и статора, кратность которых позволяет выдавать пиковый КМ (600 Нм) на любой скорости. При этом мощность электродвигателя, например, у Теслы, составляет 416 л. с.

Чтобы ответить на вопрос – дизельный, бензиновый или электродвигатель лучше, надо сначала исключить третий вариант, поскольку электродвигатели пока не так распространены, как первые два типа.

ВАЖНО! Что касается выбора между бензиновым и дизельным двигателями, они в первую очередь отличаются мощностью и крутящим моментом. На практике это означает, что при одинаковом объеме двигателя дизельный быстрее разгоняется, а бензиновый позволяет давать более высокую скорость.

Кроме того, благодаря большему крутящему момент автомобиль, использующийся как грузовой, обладает большей грузоподъемностью за счет двигателя. Особенно если двигатель дизель-генераторный.

Улучшение разгона авто за счет изменения момента вращения

Чем выше показатель крутящего момента – тем быстрее двигатель набирает мощность. Таким образом, вырастет скорость движения. На практике это означает, что, например, во время разгона крутящий момент позволит быстрее обогнать едущий впереди автомобиль.

Чтобы улучшить разгон автомобиля за счет изменения момента вращения, достаточно повысить показатели последнего. Как это сделать – описано выше.

Зависимость мощности от крутящего момента

Крутящий момент, как говорилось выше, это показатель того, с какой скоростью двигатель может набирать обороты. По сути, мощность мотора – прямая производная от КМ на коленвале. Чем больше оборотов – тем выше показатель мощности.

Зависимость мощности от вращательного момента выражается формулой: Р = М*n (Р – мощность, М – крутящий момент, n – количество оборотов коленвала/мин).

Что такое крутящий момент электродвигателя

Одним из важных параметров электродвигателя, который так же важен при его выборе, является крутящий момент. Эта величина определяется произведением приложенной к плечу рычага силы и зависит исключительно от степени нагрузки. Если в двигателях внутреннего сгорания данную нагрузку задаётся коленчатым валом, то асинхронные электродвигатели получают величину крутящего момента от токов возбуждения. При этом величина этого момента будет зависеть от скорости вращающегося в магнитном поле статора устройства, называемого ротор. В зависимости от периода и способа определения, крутящий момент разделяют на:

• статический (пусковой) – минимальный момент холостого хода;
• промежуточный – развивает значение при работе двигателя от 0 величины оборотов до максимального значения в номинальной величине напряжения;
• максимальный – развивающийся при эксплуатации двигателя;
• номинальный – соответствует номинальным значениям мощности и оборотов.

Для вычисления величины крутящего момента, определяющегося в «кгм» (килограмм на метр) или «Нм» (ньютон на метр), многие электротехнические пособия предлагают специальные формулы, учитывающие кроме основного действия вращающегося магнитного поля ряд всевозможных факторов, например:

• напряжения сети;
• величину индуктивного и активного сопротивления;
• зависимость от увеличения скольжения.

Но, рост скольжения не всегда приносит высокий момент. Зачастую, при достижении критических значений, наблюдается его резкое снижение. Такое явление обозначается как опрокидывающий момент. Одним из устройств, стабилизирующих скорость вращения ротора, а значит и величину момента кручения является частотный преобразователь, применение которого сейчас очень распространено во всех сферах, где от контроля работы двигателя зависит и успешность выполнения множественных производственных задач.

Выбираем электродвигатель по крутящему моменту

Для выбора, требуемого к выполнению тех или иных задач электродвигателя, берут в учёт практически все его характеристики, начиная от показателей мощности и заканчивая массогабаритными параметрами. Каждый из элементов по-своему важен в решении нюансов. Не меньшее значение припадает и на крутящий момент. Благодаря тому, что момент кручения напрямую связан с оборотами в соотношении: чем больше сами обороты, тем меньше будет момент, выбор электродвигателя будет исходить из следующих нюансов:

• из скоростных требований. В этом случае, более полезным будет выбор двигателя по малому моменту для работающих со слабыми усилиями и на большой скорости, и со средними либо высокими показателями моментов пуска для работающих в усиленных режимах. На малых скоростях;
• по пусковым напряжениям. Здесь учитывается первичное усилие, например, для управления лифтом следует подбирать двигатели высокого пускового момента, способного поднимать большие грузы со старта. Хотя, многие статьи про электродвигатели рекомендуют так же применять устройства плавного пуска, умеющие обезопасить от нежелательных перегрузов.

Стоит помнить, что выбор осуществляется не по одному из показателей, даже при ориентировании относительно крутящего момента, ведь каждый из показателей ориентируется по рабочей предрасположенности электротехнического приводного устройства и его рабочих нагрузок в статистических и динамических эксплуатационных условиях, задаваемых самим предприятием.

Остались вопросы?
Специалисты ЭНЕРГОПУСК ответят на Ваши вопросы:
8-800-700-11-54 (8-18, Пн-Вт)

7.2: Классическая механика

Область классической механики включает изучение тел в движении, особенно физические законы, касающиеся тел, находящихся под воздействием сил. Большинство механических аспектов проектирования роботов тесно связано с концепциями из этой области. В данном блоке описываются несколько ключевых применяемых концепций классической механики.

СКОРОСТЬ — это мера того, насколько быстро перемещается объект. Обозначает изменение положения во времени (проще говоря, какое расстояние способен преодолеть объект за заданный период времени). Данная мера представлена в единицах расстояния, взятых в единицу времени, например, в количестве миль в час или футов в секунду.

ЧАСТОТА ВРАЩЕНИЯ – Скорость может также выражаться во вращении, то есть насколько быстро объект движется по кругу. Измеряется в единицах углового перемещения во времени (то есть в градусах в секунду), или в циклах вращения в единицу времени (например, в оборотах в минуту). Когда измерения представлены в оборотах в минуту (RPM), речь идет о частоте вращения. Есть речь идет об об/мин автомобильного двигателя, это означает, что измеряется скорость вращения двигателя.

УСКОРЕНИЕ – Изменение скорости во времени представляет собой ускорение. Чем больше ускорение, тем быстрее изменяется скорость. Если автомобиль развивает скорость от 0 до 60 миль в час за две секунды, в этом случае ускорение больше, чем когда он развивает скорость от 0 до 40 миль в час за тот же период времени. Ускорение — это мера изменения скорости. Отсутствие изменения означает отсутствие ускорения. Если объект движется с постоянной скоростью — ускорение отсутствует.

СИЛА — Ускорение является следствием воздействия сил, которые провоцируют изменение в движении, направлении или форме. Если вы нажимаете на объект, это означает, что вы прикладываете к нему силу. Робот ускоряется под воздействием силы, которую его колеса прикладывают к полу. Сила измеряется в фунтах или ньютонах.

Например, масса объекта воздействует на объект как сила вследствие гравитации (ускорение объекта в направлении центра Земли).

КРУТЯЩИЙ МОМЕНТ – Сила, направленная по кругу (вращение объекта), называется крутящим моментом. Крутящий момент — это вращающая сила. Если к объекту приложен крутящий момент, на границе первого возникает линейная сила. В примере с колесом, катящемся по земле, крутящий момент, приложенный к оси колеса, создает линейную силу на границе покрышки в точке ее контакта с поверхностью земли. Так и определяется крутящий момент — как линейная сила на границе круга. Крутящий момент определяется величиной силы, умноженной на расстояние от центра вращения (Сила х Расстояние = Крутящий момент). Крутящий момент измеряется в единицах силы, умноженной на расстояние, например, фунто-дюймах или ньютон-метрах.

В примере с колесом, катящемся по земле, если известен крутящий момент, приложенный к оси с закрепленным на ней колесом, мы можем рассчитать количество силы, прикладываемой колесом к поверхности. В этом случае, радиус колеса является расстоянием силы от центра вращения.

Сила = Крутящий момент/Радиус колеса

В примере с рукой робота, удерживающей объект, мы можем рассчитать крутящий момент, требуемый для поднятия объекта. Если объект обладает массой, равной 1 ньютону, а рука имеет длину 0,25 метра (объект располагается на расстоянии 0,25 метра от центра вращения), тогда

Крутящий момент = Сила х Расстояние = 1 ньютон х 0,25 метра = 0,25 ньютон-метров.

Это означает, что для удержания объекта в неподвижном положении, необходимо применить крутящий момент, равный 0,25 ньютон-метров. Чтобы переместить объект вверх, роботу необходимо приложить к нему крутящий момент, значение которого будет превышать 0,25 ньютон-метров, так как необходимо преодолеть силу гравитации. Чем больше крутящий момент робота, тем больше силы он прикладывает к объекту, тем больше ускорение объекта, и тем быстрее рука поднимет объект.

Пример 7.2

Пример 7.3

Для данных примеров, мы можем рассчитать крутящий момент, необходимый для подъем этих объектов.

Пример 7.2 — Крутящий момент = Сила х Расстояние = 1 ньютон х 0,125 метра = 0,125 ньютон-метров.

Для данного примера, длина рука равна половине длины руки из Примера 1, поэтому значение требуемого крутящего момента также в два раза меньше. Значение длины руки пропорционально значению требуемого крутящего момента. При равных исходных характеристиках объекта, чем короче рука, тем меньший крутящий момент необходим для подъема.

Пример 7.3 — Крутящий момент = Сила * Расстояние = 1 ньютон х 0,5 метра = 0,5 ньютон-метров.

Для данного примера, длина рука равна удвоенной длине руки из Примера 1, поэтому значение требуемого крутящего момента также в два раза больше.

Еще одна точка зрения относительно ограниченного крутящего момента в соединении руки робота заключается в следующем: более короткая рука сможет поднять объект большей массы, чем более длинная рука; однако, для первой доступная высота подъема объекта будет меньше, чем для второй.

Пример 7.4

Пример 7.5

Эти примеры иллюстрируют руку робота, поднимающую объекты разной массы. Какова взаимосвязь с требуемым количеством крутящего момента?

Пример 4 — Крутящий момент = Сила х Расстояние = ½ ньютона х 0,25 метра = 0,125 ньютон-метров.

Пример 5 — Крутящий момент = Сила х Расстояние = 2 ньютона х 0,25 метра = 0,5 ньютон-метров.

Эти примеры иллюстрируют уменьшение значения требуемого крутящего момента по мере снижения массы объекта. Масса пропорциональна крутящему моменту, необходимому для ее подъема. Чем тяжелее объект, тем больше крутящий момент, требуемый для его подъема.

Проектировщики роботов должны обратить внимание на ключевые взаимосвязи между значениями крутящего момента, длины руки и массы объекта.

РАБОТА – Мера силы, приложенной на расстоянии, называется работой. Например, для удерживания объекта необходимо 10 фунтов силы. Далее, чтобы поднять этот объект на высоту 10 дюймов, требуется определенное количество работы. Количество работы, требуемое для подъема объекта на высоту 20 дюймов, удваивается. Работа также понимается как изменение энергии.

МОЩНОСТЬ — Большинство людей полагает, что мощность является термином из области электрики, но мощность также относится и к механике.

Мощность — это количество работы в единицу времени. Насколько быстро кто-то может выполнить работу?

В робототехнике принято понимать мощность как ограничение, так как соревновательные робототехнические системы имеют ограничения в части выходной мощности. Если роботу требуется поднять массу в 2 ньютона (прилагая 2 ньютона силы), скорость подъема будет ограничиваться количеством выходной мощности робота. Если робот способен произвести достаточное количество мощности, он сможет быстро поднять объект. Если он способен произвести лишь малое количество энергии, подъем объекта будет производиться медленно (либо не будет производиться вообще!).

Мощность определяется как Сила, умноженная на Скорость (насколько быстро выполняется толчок при постоянной скорости), и обычно выражается в Ваттах.

Мощность [Ватты] = Сила [Ньютоны] х Скорость [Метры в секунду]

1 Ватт = 1 (Ньютон х Метр) / Секунда

Как это применяется в соревновательной робототехнике? К проектам роботов применяются определенные ограничения. Проектировщики соревновательных роботов, использующие систему проектирования VEX Robotics Design, также должны учитывать физические ограничения, связанные с применением электромоторов. Электромотор обладает ограниченной мощностью, поэтому он может производить только определенное количество работы с заданной скоростью.

Примечание: все перспективные концепции имеют базовое описание. Более глубоко обсуждать эти физические свойства учащиеся будут в процессе обучения в ВУЗах, если выберут область STEM в качестве направления обучения.