| Динамика |
А 22. По горизонтальному столу из состояния покоя движется брусок массой 0,9 кг, соединённый с грузом массой 0,3 кг невесомой нерастяжимой нитью, перекинутой через гладкий невесомый блок (см. рисунок). Коэффициент трения бруска о поверхность стола равен 0,2. Натяжение вертикальной части нити равно |
С1-1. Два одинаковых бруска, связанные легкой пружиной, покоятся на гладкой горизонтальной поверхности стола. В момент t = 0 правый брусок начинают двигать так, что за время х он набирает конечную скорость и движется затем равномерно по прямой, совпадающей с осью пружины. За время τ левый брусок успевает сместиться значительно меньше, чем правый. Каков характер движения левого бруска относительно стола при |
С1-2. Деревянный брусок плавает на поверхности воды в миске. Миска покоится на поверхности земли. Что произойдет с глубиной погружения бруска в воду, если миска будет стоять на полу лифта, который движется с ускорением, направленным вертикально вверх? Ответ поясните, указав, какие физические явления и закономерности вы при этом использовали. |
С2-3. В сосуде (см. рисунок) находится система тел, состоящая из блока с перекинутой через него легкой нитью, к концам которой привязаны тело объёмом V и пружина жёсткостью k. Нижний конец пружины прикреплён ко дну сосуда. Как изменится сила натяжения нити, действующая на пружину, если эту систему целиком погрузить в жидкость плотностью ρ? (Считать, что трение в оси блока отсутствует.) |
С2-4. Автомобиль совершает поворот на горизонтальной дороге по дуге окружности радиуса 81 м. Какова максимальная скорость автомобиля при коэффициенте трения автомобильных шин о дорогу 0,4? |
С2-5. Грузы массами М = 1 кг и m связаны лёгкой нерастяжимой нитью, переброшенной через блок, по которому нить может скользить без трения (см. рисунок). Груз массой М находится на шероховатой наклонной плоскости (угол наклона плоскости к горизонту α = 30°, коэффициент трения μ = 0,3 |
С2.6. Брусок массой m1 = 1 кг лежит на наклонной плоскости с углом при основании, равным α = 53°. Коэффициент трения бруска с плоскостью равен μ = 0,5. К бруску привязана невесомая нить, другой конец которой перекинут через неподвижный идеальный блок. К этому концу нити подвешивается груз массой m2 = 1 кг. Определите, придет ли в движение брусок при подвешивании груза. Если придет в движение, то в каком направлении? (sin 53° = 0,8; cos 53° = 0,6) |
| С2-7. Грузовой автомобиль со всеми ведущими осями массой М = 4 т тянет за нерастяжимый трос вверх по уклону легковой автомобиль массой m = 1 т, у которого выключен двигатель. С каким максимальным ускорением могут двигаться автомобили, если угол уклона составляет α = arcsin 0,1, а коэффициент трения между шинами грузового автомобиля и дорогой μ = 0,2? Силой трения качения, действующей на легковой автомобиль, пренебречь. Массой колес пренебречь. |
С2-8. На наклонной плоскости находится брусок, связанный с грузом перекинутой через блок нерастяжимой нитью (см. рисунок). Угол наклона а плоскости равен 30°, масса бруска — 2 кг, коэффициент трения бруска о плоскость равен 0,23, масса груза — |
С2-9. Система грузов M, m1 и m2 показанная на рисунке, движется из состояния покоя. Поверхность стола — горизонтальная гладкая. Коэффициент трения между грузами M и m1 равен μ = 0,2. Грузы М и m2 связаны легкой нерастяжимой нитью, которая скользит по блоку без трения. Пусть M = 1.2 кг, m1 = m2 = m. При каких значениях m грузы M и m1 движутся как одно целое? |
С2-10. Материальные точки массами m1 = 100 г и m2 = 200 г прикреплены к невесомому стержню, как показано на рисунке. К точке m2 прикреплена невесомая пружина жесткостью k = 30 Н/м, верхний конец которой закреплен. Длина пружины в недеформированном состоянии l |
С2-11. В аттракционе человек массой 70 кг движется на тележке по рельсам и совершает «мертвую петлю» в вертикальной плоскости. Каков радиус круговой траектории, если в верхней точке сила давления человека на сидение тележки равна 700 Н при скорости движения тележки 10 м/с? Ускорение свободного падения принять равным 10 м/с2. |
С2-12. В аттракционе человек массой 80 кг движется на тележке по рельсам и совершает «мертвую петлю» в вертикальной плоскости. Каков радиус круговой траектории, если в верхней точке сила давления человека на сидение тележки равна 200 Н при скорости движения тележки 7,5 м/с? Ускорение свободного падения принять равным 10 м/с2. |
С2.13.В аттракционе человек массой 80 кг движется на тележке по рельсам и совершает «мертвую петлю» в вертикальной плоскости. Каков радиус круговой траектории, если при скорости 10 м/с, направленной вертикально вверх, сила нормального давления человека на сидение тележки равна 1600 Н? Ускорение свободного падения равно 10 м/с |
С2.14. В аттракционе человек массой 60 кг движется на тележке по рельсам и совершает «мертвую петлю» в вертикальной плоскости. Какова сила давления человека на сидение тележки в нижней точке при движении тележки со скоростью 10 м/с, если радиус круговой траектории 10 м? Ускорение свободного падения принять равным 10 м/с2. |
С2-15. В аттракционе человек массой 100 кг совершает «мертвую петлю» в вертикальной плоскости. Когда вектор скорости был направлен вертикально вниз, сила нормального давления человека на сидение была 2000 Н. Найдите скорость тележки в этой точке при радиусе круговой траектории 5 м. Ускорение свободного падения 10 м/с2. |
С2.16. В аттракционе человек движется на тележке по рельсам и совершает «мертвую петлю» в вертикальной плоскости. С какой скоростью должна двигаться тележка в верхней точке круговой траектории радиусом 6,4 м, чтобы в этой точке сила давления человека на сидение тележки была равна 0 Н? Ускорение свободного падения 10 м/с2. |
С2.17. В аттракционе человек движется на тележке по рельсам и совершает «мертвую петлю» в вертикальной плоскости. С какой скоростью должна двигаться тележка в верхней точке круговой траектории радиусом 4,9 м, чтобы в этой точке сила давления человека на сидение тележки была равна |
С2.18. В аттракционе человек массой 70 кг движется на тележке по рельсам и совершает «мертвую петлю» в вертикальной плоскости. С какой скоростью движется тележка в верхней точке круговой траектории радиусом 5 м, если в этой точке сила давления человека на сидение тележки равна 700 Н? Ускорение свободного падения принять равным 10 м/с2. |
С2.19. В аттракционе человек массой 70 кг движется на тележке по рельсам и совершает «мертвую петлю» в вертикальной плоскости. С какой скоростью двигалась тележка в нижней точке круговой траектории радиусом 5 м, если в этой точке сила давления человека на сидение тележки была равна 2100 Н? Ускорение свободного падения 10 м/с2. |
С2-20. Шарик скользит без трения по наклонному желобу, а затем движется по «мертвой петле» радиусом R. С какой силой шарик давит на желоб в нижней точке петли, если масса шарика равна 100 г, а высота, с которой его отпускают, равна 4R? |
С2-21. Средняя плотность планеты Плюк равна средней плотности Земли, а первая космическая скорость для Плюка в 2 раза больше, чем для Земли. Чему равно отношение периода обращения спутника, движущегося вокруг Плюка по низкой круговой орбите, к периоду обращения аналогичного спутника Земли? Объем шара пропорционален кубу радиуса (V ~ R3). |
С2-22. Радиус планеты Плюк в 2 раза меньше радиуса Земли, а период обращения спутника, движущегося вокруг Плюка по низкой круговой орбите, совпадает с периодом обращения аналогичного спутника Земли. Чему равно отношение средних плотностей Плюка и Земли? Объём шара пропорционален кубу радиуса (V ~ R3). |
С2-23. Масса Марса составляет 0,1 массы Земли, диаметр у Марса вдвое меньше, чем у Земли. Каково отношение периодов обращения искусственных спутников Марса и Земли —TМ / TЗ, движущихся по круговым орбитам на небольшой высоте? |
С2-24. К покоящемуся на шероховатой горизонтальной поверхности телу приложена нарастающая с течением времени горизонтальная сила тяги F = bt, где b — постоянная величина. На рисунке представлен график зависимости ускорения тела от времени действия силы. Определите коэффициент трения скольжения. |
С2-25. Полый конус с углом при вершине 2α вращается с угловой скоростью ω вокруг вертикальной оси, совпадающей с его осью симметрии. Вершина конуса обращена вверх. На внешней поверхности конуса находится небольшая шайба, коэффициент трения которой о поверхность конуса равен μ. При каком максимальном расстоянии L от вершины шайба будет неподвижна относительно конуса? Сделайте схематический рисунок с указанием сил, действующих на шайбу. |
С2-26. Полый конус с углом при вершине 2α вращается с угловой скоростью ω вокруг вертикальной оси, совпадающей с его осью симметрии. Вершина конуса обращена вверх. На внешней поверхности конуса находится небольшая шайба. При каком минимальном коэффициенте трения шайба будет неподвижна относительно конуса на расстоянии L от вершины конуса? Сделайте схематический рисунок с указанием сил, действующих на шайбу |
С2-27. Полый конус с углом при вершине 2α вращается вокруг вертикальной оси, совпадающей с его осью симметрии. Вершина конуса обращена вверх. На внешней поверхности конуса находится небольшая шайба, коэффициент трения которой о поверхность конуса равен μ. При какой максимальной угловой скорости вращения конуса шайба будет неподвижна относительно конуса, находясь на расстоянии L от вершины? Сделайте рисунок с указанием сил, действующих на шайбу. |
| Динамика (примеры решения задач повышенного уровня сложности) |
С1-1. Два одинаковых бруска, связанные легкой пружиной, покоятся на гладкой горизонтальной поверхности стола. В момент t = 0 правый брусок начинают двигать так, что за время х он набирает конечную скорость и движется затем равномерно по прямой, совпадающей с осью пружины. За время τ левый брусок успевает сместиться значительно меньше, чем правый. Каков характер движения левого бруска относительно стола при t > τ? Ответ поясните, указав, какие физические явления и закономерности вы при этом использовали. |
С1-2. Деревянный брусок плавает на поверхности воды в миске. Миска покоится на поверхности земли. Что произойдет с глубиной погружения бруска в воду, если миска будет стоять на полу лифта, который движется с ускорением, направленным вертикально вверх? Ответ поясните, указав, какие физические явления и закономерности вы при этом использовали. |
С2-3. В сосуде (см. рисунок) находится система тел, состоящая из блока с перекинутой через него легкой нитью, к концам которой привязаны тело объёмом V и пружина жёсткостью k. Нижний конец пружины прикреплён ко дну сосуда. Как изменится сила натяжения нити, действующая на пружину, если эту систему целиком погрузить в жидкость плотностью ρ? (Считать, что трение в оси блока отсутствует.) |
С2-4. Автомобиль совершает поворот на горизонтальной дороге по дуге окружности радиуса 81 м. Какова максимальная скорость автомобиля при коэффициенте трения автомобильных шин о дорогу 0,4? |
С2-5. Грузы массами М = 1 кг и m связаны лёгкой нерастяжимой нитью, переброшенной через блок, по которому нить может скользить без трения (см. рисунок). Груз массой М находится на шероховатой наклонной плоскости (угол наклона плоскости к горизонту α = 30°, коэффициент трения μ = 0,3). Чему равно максимальное значение массы m, при котором система грузов ещё не выходит из первоначального состояния покоя? |
С2.6. Брусок массой m1 = 1 кг лежит на наклонной плоскости с углом при основании, равным α = 53°. Коэффициент трения бруска с плоскостью равен μ = 0,5. К бруску привязана невесомая нить, другой конец которой перекинут через неподвижный идеальный блок. К этому концу нити подвешивается груз массой m2 = 1 кг. Определите, придет ли в движение брусок при подвешивании груза. Если придет в движение, то в каком направлении? (sin 53° = 0,8; cos 53° = 0,6) |
С2-7. Грузовой автомобиль со всеми ведущими осями массой М = 4 т тянет за нерастяжимый трос вверх по уклону легковой автомобиль массой m = 1 т, у которого выключен двигатель. С каким максимальным ускорением могут двигаться автомобили, если угол уклона составляет α = arcsin 0,1, а коэффициент трения между шинами грузового автомобиля и дорогой μ = 0,2? Силой трения качения, действующей на легковой автомобиль, пренебречь. Массой колес пренебречь. |
С2-8. На наклонной плоскости находится брусок, связанный с грузом перекинутой через блок нерастяжимой нитью (см. рисунок). Угол наклона а плоскости равен 30°, масса бруска — 2 кг, коэффициент трения бруска о плоскость равен 0,23, масса груза — 0,2 кг. В начальный момент времени брусок покоился на расстоянии 5 м от точки А у основания плоскости. Определите расстояние от бруска до точки А через 2 с после начала движения. |
С2-9. Система грузов M, m1 и m2 показанная на рисунке, движется из состояния покоя. Поверхность стола — горизонтальная гладкая. Коэффициент трения между грузами M и m1 равен μ = 0,2. Грузы М и m2 связаны легкой нерастяжимой нитью, которая скользит по блоку без трения. Пусть M = 1.2 кг, m1 = m2 = m. При каких значениях m грузы M и m1 движутся как одно целое? |
С2-10. Материальные точки массами m1 = 100 г и m2 = 200 г прикреплены к невесомому стержню, как показано на рисунке. К точке m2 прикреплена невесомая пружина жесткостью k = 30 Н/м, верхний конец которой закреплен. Длина пружины в недеформированном состоянии l0 = 20 см. В начальный момент концы пружины связаны нитью длиной l = 10 см. Определите силу реакции стержня, действующую на массу m2 сразу после пережигания нити. |
С2-11. В аттракционе человек массой 70 кг движется на тележке по рельсам и совершает «мертвую петлю» в вертикальной плоскости. Каков радиус круговой траектории, если в верхней точке сила давления человека на сидение тележки равна 700 Н при скорости движения тележки 10 м/с? Ускорение свободного падения принять равным 10 м/с2. |
С2-12. В аттракционе человек массой 80 кг движется на тележке по рельсам и совершает «мертвую петлю» в вертикальной плоскости. Каков радиус круговой траектории, если в верхней точке сила давления человека на сидение тележки равна 200 Н при скорости движения тележки 7,5 м/с? Ускорение свободного падения принять равным 10 м/с2. |
С2.13.В аттракционе человек массой 80 кг движется на тележке по рельсам и совершает «мертвую петлю» в вертикальной плоскости. Каков радиус круговой траектории, если при скорости 10 м/с, направленной вертикально вверх, сила нормального давления человека на сидение тележки равна 1600 Н? Ускорение свободного падения равно 10 м/с2. |
С2.14. В аттракционе человек массой 60 кг движется на тележке по рельсам и совершает «мертвую петлю» в вертикальной плоскости. Какова сила давления человека на сидение тележки в нижней точке при движении тележки со скоростью 10 м/с, если радиус круговой траектории 10 м? Ускорение свободного падения принять равным 10 м/с2. |
С2-15. В аттракционе человек массой 100 кг совершает «мертвую петлю» в вертикальной плоскости. Когда вектор скорости был направлен вертикально вниз, сила нормального давления человека на сидение была 2000 Н. Найдите скорость тележки в этой точке при радиусе круговой траектории 5 м. Ускорение свободного падения 10 м/с2. |
С2.16. В аттракционе человек движется на тележке по рельсам и совершает «мертвую петлю» в вертикальной плоскости. С какой скоростью должна двигаться тележка в верхней точке круговой траектории радиусом 6,4 м, чтобы в этой точке сила давления человека на сидение тележки была равна 0 Н? Ускорение свободного падения 10 м/с2. |
С2.17. В аттракционе человек движется на тележке по рельсам и совершает «мертвую петлю» в вертикальной плоскости. С какой скоростью должна двигаться тележка в верхней точке круговой траектории радиусом 4,9 м, чтобы в этой точке сила давления человека на сидение тележки была равна 0 Н? Ускорение свободного падения 10 м/с2. |
С2.18. В аттракционе человек массой 70 кг движется на тележке по рельсам и совершает «мертвую петлю» в вертикальной плоскости. С какой скоростью движется тележка в верхней точке круговой траектории радиусом 5 м, если в этой точке сила давления человека на сидение тележки равна 700 Н? Ускорение свободного падения принять равным 10 м/с2. |
С2.19. В аттракционе человек массой 70 кг движется на тележке по рельсам и совершает «мертвую петлю» в вертикальной плоскости. С какой скоростью двигалась тележка в нижней точке круговой траектории радиусом 5 м, если в этой точке сила давления человека на сидение тележки была равна 2100 Н? Ускорение свободного падения 10 м/с2. |
С2-20. Шарик скользит без трения по наклонному желобу, а затем движется по «мертвой петле» радиусом R. С какой силой шарик давит на желоб в нижней точке петли, если масса шарика равна 100 г, а высота, с которой его отпускают, равна 4R? |
С2-21. Средняя плотность планеты Плюк равна средней плотности Земли, а первая космическая скорость для Плюка в 2 раза больше, чем для Земли. Чему равно отношение периода обращения спутника, движущегося вокруг Плюка по низкой круговой орбите, к периоду обращения аналогичного спутника Земли? Объем шара пропорционален кубу радиуса (V ~ R3). |
С2-22. Радиус планеты Плюк в 2 раза меньше радиуса Земли, а период обращения спутника, движущегося вокруг Плюка по низкой круговой орбите, совпадает с периодом обращения аналогичного спутника Земли. Чему равно отношение средних плотностей Плюка и Земли? Объём шара пропорционален кубу радиуса (V ~ R3). |
С2-23. Масса Марса составляет 0,1 массы Земли, диаметр у Марса вдвое меньше, чем у Земли. Каково отношение периодов обращения искусственных спутников Марса и Земли —TМ / TЗ, движущихся по круговым орбитам на небольшой высоте? |
С2-24. К покоящемуся на шероховатой горизонтальной поверхности телу приложена нарастающая с течением времени горизонтальная сила тяги F = bt, где b — постоянная величина. На рисунке представлен график зависимости ускорения тела от времени действия силы. Определите коэффициент трения скольжения. |
С2-25. Полый конус с углом при вершине 2α вращается с угловой скоростью ω вокруг вертикальной оси, совпадающей с его осью симметрии. Вершина конуса обращена вверх. На внешней поверхности конуса находится небольшая шайба, коэффициент трения которой о поверхность конуса равен μ. При каком максимальном расстоянии L от вершины шайба будет неподвижна относительно конуса? Сделайте схематический рисунок с указанием сил, действующих на шайбу. |
С2-26. Полый конус с углом при вершине 2α вращается с угловой скоростью ω вокруг вертикальной оси, совпадающей с его осью симметрии. Вершина конуса обращена вверх. На внешней поверхности конуса находится небольшая шайба. При каком минимальном коэффициенте трения шайба будет неподвижна относительно конуса на расстоянии L от вершины конуса? Сделайте схематический рисунок с указанием сил, действующих на шайбу |
С2-27. Полый конус с углом при вершине 2α вращается вокруг вертикальной оси, совпадающей с его осью симметрии. Вершина конуса обращена вверх. На внешней поверхности конуса находится небольшая шайба, коэффициент трения которой о поверхность конуса равен μ. При какой максимальной угловой скорости вращения конуса шайба будет неподвижна относительно конуса, находясь на расстоянии L от вершины? Сделайте рисунок с указанием сил, действующих на шайбу. |
Методический материал к уроку решения задач по динамике
Наклонная плоскость с трением
Вариант 1.
С вершины наклонной плоскости высотой 5 м и углом наклона 45º начинает соскальзывать тело. Найти скорость тела в конце спуска, если коэффициент трения тела о плоскость равен 0,19.
Телу толчком сообщили скорость 3 м/с, направленную вдоль наклонной плоскости. Найти время движения тела вверх до остановки, если синус угла наклона плоскости к горизонту 0,6, а коэффициент трения 0,25.
Тело поднимают вверх вдоль наклонной плоскости, прикладывая к нему горизонтальную силу, величина которой в два раза больше действующей на тело силы тяжести. Высота наклонной плоскости равна 3 м, ее длина равна 5 м. Найти ускорение тела, если коэффициент трения равен 0,2..
Вариант 2.
Тело соскальзывает с наклонной плоскости с наклонной плоскости высотой 5 м и длиной 13 м. Коэффициент трения равен 0,4. Найти время движения тела вдоль наклонной плоскости.
Телу толчком сообщили скорость, направленную вдоль наклонной плоскости. Найти величину ускорения тела, если высота наклонной плоскости 4 м, ее длина 5 м, коэффициент трения равен 0,5.
С каким ускорением начнет спускаться тело с наклонной плоскости, если за привязанную к телу нить потянуть в горизонтальном направлении с силой в два раза меньше действующей на тело силы тяжести. Высота наклонной плоскости 3 м, ее длина 5 м. Коэффициент трения равен 0,8.
Силы сопротивления в задачах динамики
Задача 1. Мяч, брошенный с поверхности земли вертикально вверх со скоростью v₀ = 10 м/с, упал на землю. За время полета скорость мяча уменьшилась по величине на 30%. Найдите продолжительность T полета мяча. Силу сопротивления считайте пропорциональной скорости: F=-kv.
Задача 2. Лодку массой 100 кг тянут за веревку по поверхности озера с постоянной скоростью 1 м/с. В некоторый момент времени веревка обрывается.. Какой путь пройдет после этого лодка до полной остановки? Считайте, что сила сопротивления зависит от скорости и ускорения лодки по закону F=- (αυ +βa), где α=10 Нс/м, β=50 Нс2/м
Задача 3. На горизонтальной поверхности покоится брусок. Черепаха перемещается с одного конца этого бруска на другой. Найдите расстояние, пройденное бруском за все время движения черепахи. Силу сопротивления считайте пропорциональной скорости бруска относительно горизонтальной поверхности: FС=-kv.
Задача 4. На горизонтальном столе один на другом лежат три длинных бруска. Массы брусков m. Бруски смазаны маслом. При движении сила трения между брусками, а также между нижним бруском и столом пропорциональна относительной скорости: F=- kv0. Сначала все бруски неподвижны, затем верхнему бруску сообщают горизонтальную скорость v. Определите относительные смещения брусков после прекращения движения.
Динамика-2
Задача 1. К концу висящей вертикально пружины, массой которой можно пренебречь, подвешен груз массой m. Затем к середине уже растянутой пружины подвешивают еще один груз той же массы. Определить длину уже растянутой пружины. Жесткость пружины равна k , а ее длина в нерастянутом состоянии равна ℓ0.
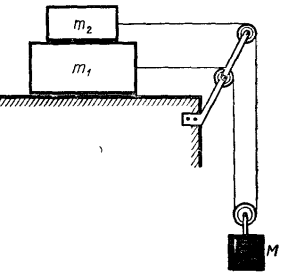
Задача 2. На горизонтальной плоскости лежит брусок массой m1, а на нем другой брусок массой m2. Через систему блоков перекинута нить. К подвижному блоку подвешен груз массой M=m1+m2. При каком соотношении между массами m1 и m2 бруски не будут скользить друг по другу, если коэффициент трения между брусками равен µ, а коэффициент трения нижнего бруска о плоскость равен нулю. Нить нерастяжима и невесома, трения в блоках нет.
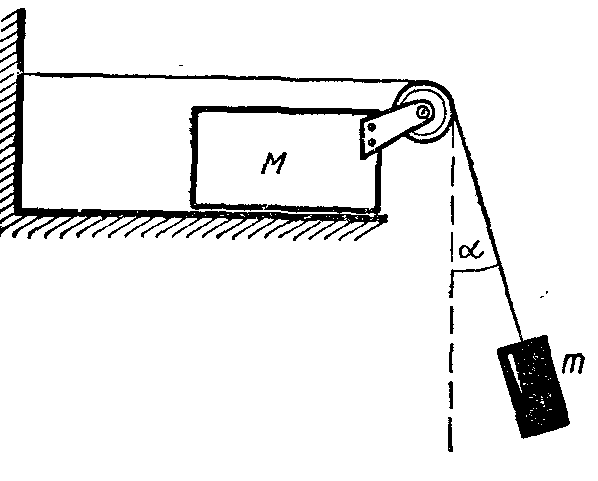
Задача 4. В механической системе брусок массой M может скользить по рельсам без трения. В начальный момент, подвешенный на нити груз, отводят от вертикали на угол αи отпускают. Найти массу этого груза, если угол, образованный нитью с вертикалью, не меняется при движении системы?
Динамика-1.
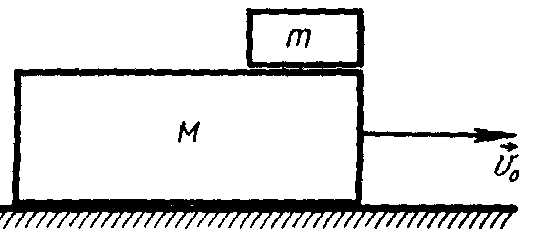
Задача 1. На конце доски длиной L и массой M находится короткий брусок массой m . Доска может скользить без трения по горизонтальной плоскости. Коэффициент трения скольжения бруска по поверхности доски равен µ. Какую скорость нужно толчком сообщить доске, чтобы она выскользнула из-под доски?
Задача 2.На доске массой 4 кг, лежащей на горизонтальном полу, находится брусок массой 1 кг. Коэффициент трения между бруском и доской равен 0,2, а между доской и полом 0,4. Какую наименьшую горизонтальную силу надо приложить к доске, чтобы брусок с нее соскользнул?
Задача 3. На доске массой 2 кг, лежащей на гладкой горизонтальной поверхности, находится брусок массой 1 кг. Коэффициент трения между доской и бруском равен 0,4. Какую наименьшую силу нужно приложить к бруску, чтобы стащить его с доски?
Задача 4. Доска массой 8 кг может двигаться без трения по наклонной плоскости с углом наклона 30º к горизонту. С каким ускорением может бежать по доске человек массой 80 кг, чтобы доска не соскальзывала с наклонной плоскости?
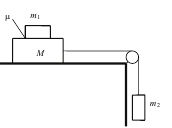
Задача 5. Система грузов M, m1 и m2, показанная на рисунке, движется из состояния покоя. Поверхность стола – горизонтальная гладкая. Коэффициент трения между грузами M и m1 равен μ = 0,2. Грузы M и m2 связаны легкой нерастяжимой нитью, которая скользит по блоку без трения. Пусть m1 = m2 = m = 0,5 кг. При каких значениях M грузы M и m1 движутся как одно целое?
Задача 6. Грузовой автомобиль со всеми ведущими осями массой 4 т тянет за нерастяжимый трос вверх по склону легковой автомобиль с выключенным двигателем. Автомобили движутся с ускорением 0,6 м /с2. Какова максимально возможная масса m легкового автомобиля, если угол уклона α = arcsin 0,1, а коэффициент трения между шинами грузового автомобиля и дорогой 0,2? Силой трения, действующей на легковой автомобиль, массой колёс и массой троса пренебречь. Считать, что трос натянут параллельно склону.
Динамика-2
Задача 1. Призме А, на которой находится брусок В, сообщили ускорение a. При каком максимальном значении этого ускорения, брусок будет оставаться еще неподвижным относительно призмы, если µ<ctg α.
Задача 2. На клине с углом наклона α лежит монета. С каким минимальным ускорением должен двигаться клин, чтобы монета свободно падала вниз?
Задача 3. Клин массой М с углом наклона α может свободно двигаться по горизонтальной поверхности. На нем расположен другой клин массой m с таким же углом α так, что его верхняя поверхность горизонтальна. Какую горизонтальную силу нужно приложить к нижнему клину, чтобы верхний клин оставался на одной и той же высоте? Трения между клиньями нет.
Задача 4. С каким горизонтальным ускорением должен двигаться клин с углом наклона α, чтобы лежащий на нем груз массой m, поднимался вверх, если коэффициент трения между грузом и клином равен µ
Статика-1
Под каким минимальным углом к горизонту может стоять однородная лестница, прислоненная к гладкой стене, если коэффициент трения между лестницей и полом равен µ.
Лестница опирается на вертикальную стену и горизонтальный пол. Коэффициент трения между лестницей и стеной равен 0,5, а между полом и лестницей равен 0,4. Найти угол наклона лестницы, при котором она находится в равновесии.
К стене прислонена лестница массой m. Центр тяжести лестницы находится на расстоянии 1/3 длины от ее верхнего конца. Какую горизонтальную силу нужно приложить к середине лестницы, чтобы ее верхний конец не давил на стену?
Однородный шар подвешен на нити, конец которой закреплен на вертикальной стене. Каким должен быть коэффициент трения между шаром и стенкой, чтобы точка крепления нити к шару и центр шара могли находиться на одной вертикали? Радиус шара R, длина нити ℓ.
Колесо радиусом R и массой m стоит перед ступенькой высоты h. Какую горизонтальную минимальную силу нужно приложить к оси колеса, чтобы оно могло приподняться на ступеньку?
Каков должен быть коэффициент трения для того, чтобы клин, заколоченный в бревно, не выскакивал из него. Угол при вершине клина равен 60º.
Однородная тонкая пластинка имеет форму круга радиусом R, в котором вырезано отверстие радиусом R/2. Где находится центр тяжести такой пластины?
В вершинах треугольника АВС находятся массы 4, 6, 10 г. АВ=50 см, ВС=40 см, СА= 30 см. На каком расстоянии от ВС находится центр тяжести системы?
Многоуровневые задания по теме «Динамика»
Министерство образования и науки Самарской области
Государственное автономное образовательное учреждение дополнительного профессионального образования (повышения квалификации) специалистов
САМАРСКИЙ ОБЛАСТНОЙ ИНСТИТУТ ПОВЫШЕНИЯ КВАЛИФИКАЦИИ
И ПЕРЕПОДГОТОВКИ РАБОТНИКОВ ОБРАЗОВАНИЯ
Итоговая работа
На курсах повышения квалификации
(30.03-3.04.2015.)
Разработка многоуровневой системы задач
по теме «Динамика»
Выполнила:
Пышкина Надежда Васильевна,
учитель физики ГБОУ СОШ пос.Светлодольск
Сергиевского района Самарской области
Сергиевск
2015 г.
+
Пояснительная записка
ФИО (полностью)
Пышкина Надежда Васильевна
Место работы
Государственное бюджетное общеобразовательное учреждение средняя общеобразовательная школа пос.Светлодольск
Должность
Учитель физики
Предмет
Физика
Класс
7 — 11
Цель: формирование умений и навыков, отработку различных способов действий при решении комбинированных задач по физике .
Задачи:
— обучающие: осмысливать и анализировать текст задачи, произвольное построение речевого высказывания, постановка и формулирование проблемы, выдвижение гипотез и их обоснование, самостоятельное выделение и формулирование познавательной цели, построение логической цепочки рассуждений, выбор наиболее эффективного способа решения задач и критическое оценивание полученного ответа;
-развивающие: целеполагание, планирование своей деятельности в зависимости от конкретных условий; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности, саморегуляция, развитие творческой и мыслительной деятельности учащихся, развитие интеллектуальных качеств, самостоятельности, гибкости мышления;
-воспитательные: смыслообразование, умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, воспитывать ответственность и аккуратность.
Технология разработки многоуровневой системы задач, позволяет ученикам успешно освоить программу как на базовом, так и на углублённом уровнях, эффективно подготовиться к государственной аттестации в форме ЕГЭ. Кратко описана методика применения этой системы.
В предлагаемом подходе предлагается в каждом разделе школьного курса физики выделить максимально полный Перечень элементов содержания образования (понятий, теорем, приёмов решения задач определённого типа и способов общеучебной деятельности) и построить соответствующую этому Перечню многоуровневую систему учебных физических задач с охватом базового и углубленного уровней.
Это позволяет на основе задачного подхода разработать методику обучения физике, позволяющую строить для каждого учащегося индивидуальные образовательные траектории, направленные как на формирование специальных, так и универсальных учебных действий, на успешную подготовку к итоговому государственному экзамену, к вступительным экзаменам в вузы, тем самым, в рамках учебного курса решить проблему качественного обучения физики в средней школе.
Учебная деятельность при решении задач, относящихся к 1 уровню — носит репродуктивный характер (используются такие общеучебные действия, как классификация, подведение под понятие, выведение следствий, действия, построение логической цепи рассуждений, и т.д.).
При решении задач относящихся ко 2 уровню – учащимся необходимо применить формулу, закон или правило. (Простые задачи на 1 действие).
При решении задач 3 уровня – учащимся необходимо применить 2-3 формулы, это задачи на 2-3 действия. (Здесь проявляются такие общеучебные действия, как выделение и формулирование познавательной цели, поиск и выделение необходимой информации, знаково-символические действия, включая математическое моделирование, структурирование знания).
Наконец, при решении задач 4 уровня учебная деятельность носит углубленный характер. Ученик должен уметь ориентироваться в новых ситуациях и вырабатывать принципиально новые программы действий (выдвигать гипотезу, проверять: обосновывать или опровергать, выдвигать новую и т.д., осуществлять исследовательскую деятельность). Решение таких задач требует от учащегося обладания обширным фондом отработанных и быстро развертываемых алгоритмов; умения оперативно перекодировать информацию из знаково-символической формы в графическую и, наоборот, из графической в знаково-символическую; системного видения курса. Вместе с тем, оно не просто предполагает использование старых алгоритмов в новых условиях и возрастание технической сложности, а отличается неочевидностью применения и комбинирования изученных алгоритмов. Задания 4 уровня содержат внутри себя составные звенья заданий из 1-3 уровней. Таким образом, учащийся, выполнив все предложенные задания, и пройдя весь путь от простого к сложному, получает умения и навыки работы с комбинированными задачами.
Особо можно выделить раздел качественных задач, содержащих как теоретическое, так и практическое обоснование решения задачи.
1. уровень — Понятийный
1
Парашютист спускается по вертикали с постоянной скоростью 2м/с. Систему отсчета, связанную с Землей, считать инерциальной. В этом случае
На парашютиста не действуют никакие силы
Сила тяжести, действующая на парашютиста, равна нулю
Сумма сил, приложенных к парашютисту, равна нулю
Сумма всех сил, действующих на парашютиста, постоянна и не равна нулю
Ответ 3
2
Выберите формулу второго закона Ньютона.
F=mа
а=Fm
F=m/а
F=mg
Ответ 1
3
Пуля пробила мишень и полетела дальше. При этом
Сила удара пули по модулю больше силы удара по ней мишени
Сила удара пули может быть больше или меньше модуля силы удара по ней мишени в зависимости от материала мишени
Сила удара мишени по пуле по модулю больше силы удара по ней пули
Сила удара пули по мишени по модулю равна силе удара мишени по пуле
Ответ 4
4
К каждой позиции первого столбика подберите соотвествующую позицию второго столбика
Физическая величина формула
А) сила тяжести 1)F=кх
Б) сила упругости 2) F=кN
В) сила трения 3) F=mg
4) F=mа
Ответ А-3 Б-1 В-2
5
Определите к какому типу сил относятся следующие силы. Цифры могут повторяться.
Сила тип силы
А) сила тяжести 1) ядерные
Б) сила трения 2) электромагнитные
В) сила упругости 3) гравитационные
Ответ А-3 Б-2 В-2
2. уровень — Базовый
1
На тело действуют две силы под прямым углом. Равнодействующая этих сил равна 50Н. Чему равна вторая сила? Первая сила равна 40Н.
10Н
90Н
30Н
Ответ 3
2
Тело массой 20 кг равноускоренно скатывается с горки. При этом скорость тела за каждую секунду увеличивается на 2 м/с. Равнодействующая всех сил, действующих на тело, равна
1)20Н
2)30Н
3)40Н
4)60Н
Ответ 3
3
К пружине школьного динамометра подвешен груз массой 0,1 кг. При этом пружина удлинилась на 2,5 см. Каким будет удлинение пружины при добавлении еще двух грузов по 0,1 кг?
1)5 см
2)7,5 см
3)10 см
4)12,5 см
Ответ 2
4
Конькобежец массой 70 кг скользит по льду. Какова сила трения, действующая на конькобежца, если коэффициент трения скольжения коньков по льду равен 0,02?
1)0,35 Н
2)1,4 Н
3)3,5 Н
4)14 Н
Ответ 4
5
Космическая ракета удаляется от Земли. На каком расстоянии от земной поверхности сила гравитационного притяжения ракеты Землей уменьшится в 4 раза по сравнению с силой притяжения на земной поверхности? ( расстояние выражается в радиусах Земли)
1)R
2)2R
3)3R
4)4R
Ответ 1
уровень — повышенный
1
Мальчик съезжает с горки высотой 3 м на санках. Коэффициент трения полозьев санок о снег равен 0,05. Каково ускорение санок, если расстояние от вершины горки до ее основания равно 5 м?
1)1,5 м/с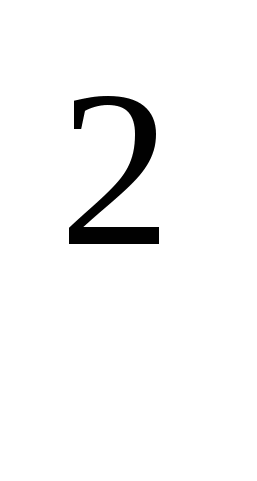
2)3,8 м/с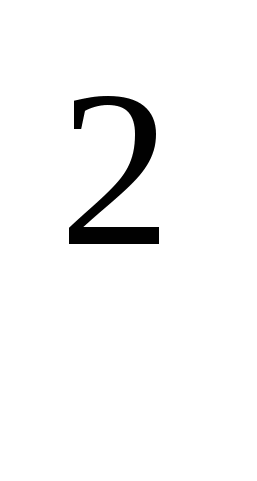
3)5,6 м/с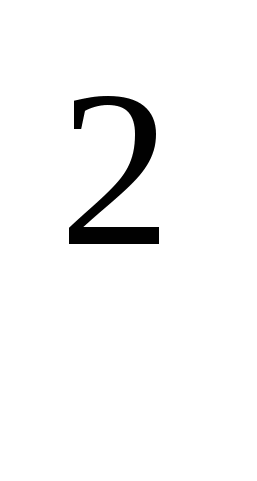
4)10 м/с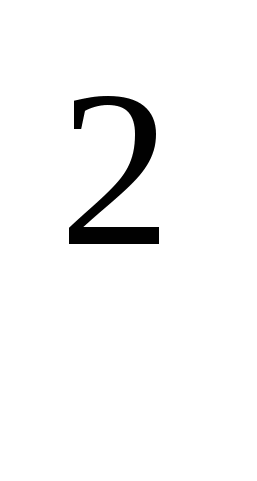

Ответ 3
2
После удара шайба массой 0,15 кг скользит по ледяной площадке. Ее скорость при этом меняется с течением времени по закону v(t)=20-3t, где все величины выражены в СИ. Коэффициент трения шайбы о лед равен
1)0,15
2)0,2
3)3
4)0,3
Ответ 4
3
Брусок массой 400 г прижат к вертикальной стене силой 4 Н. Коэффициент трения скольжения бруска по стене равен 0,5. Какую силу, направленную вверх, нужно приложить к бруску, чтобы он перемещался вверх?
1)6 Н
2)5 Н
3)10 Н
4)4 Н
Ответ 1
4
К нижнему концу пружины подвешены связанные невесомой нитью грузы: верхний массой 0,4 кг и нижний массой 0,6 кг. Нить, соединяющую грузы, пережигают. С каким ускорением начинает двигаться верхний груз?
1)10 м/с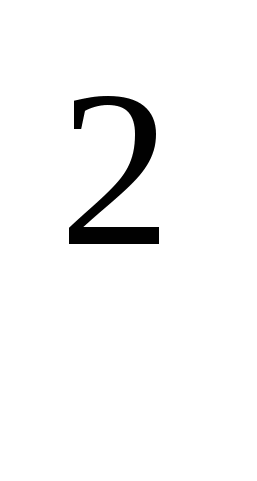
2)15 м/с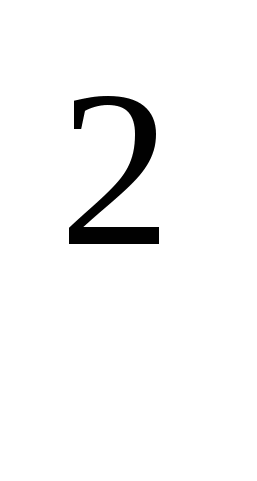
3)5 м/с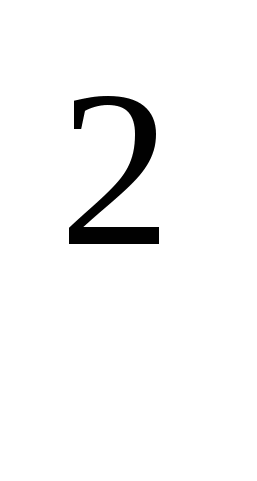
4)12 м/с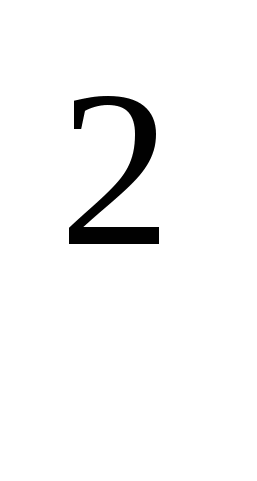

Ответ 2
5
Средняя плотность планеты Плюк равна средней плотности Земли, а радиус Плюка в 2 раза больше радиуса Земли. Во сколько раз первая космическая скорость для Плюка больше, чем для Земли?
1)3
2)1
3)2
4)4
Ответ 3
4 уровень — углубленный
1. Шайба скользит без трения по наклонному желобу, а затем движется по мертвой петле радиусом R. С какой силой шайба давит на желоб в нижней точке петли, если масса шайбы равна 100 г, а высота, с которой ее отпускают, равна 4R?
Решение: Согласно второму закону Ньютона в нижней точке петли: N=ma+mg, где m, N- соответственно, масса шайбы и сила ее давления на желоб, а – центростремительное ускорение шайбы. Причем a=v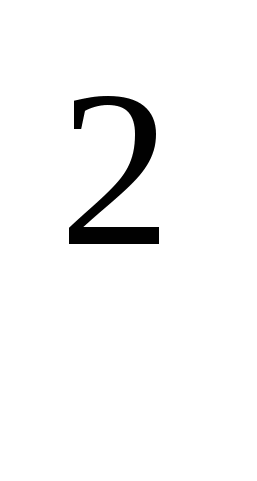 /R, где R и v – соответственно, радиус петли и скорость шайбы в нижней ее точке.
/R, где R и v – соответственно, радиус петли и скорость шайбы в нижней ее точке.
Согласно закону сохранения механической энергии mgh=mv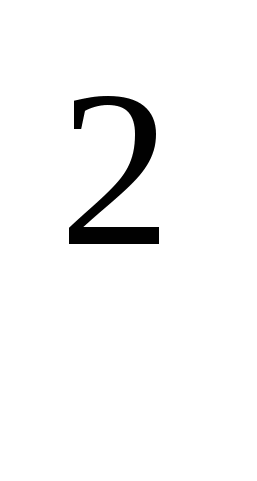 /2, где h=4R. Следовательно, N= mg +mv
/2, где h=4R. Следовательно, N= mg +mv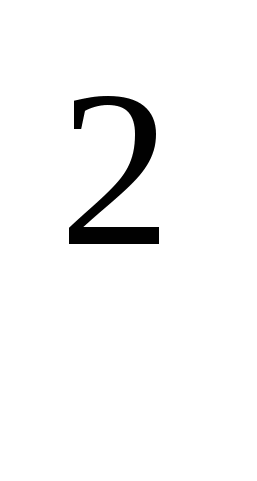 /R = mg +8mg =9H.
/R = mg +8mg =9H.
2. Грузовой автомобиль со всеми ведущими осями массой М=4т тянет за нерастяжимый трос вверх по уклону легковой автомобиль m=1т, у которого выключен двигатель. С каким максимальным ускорением могут двигаться автомобили, если угол уклона составляет a = arsin 0.1, а коэффициент трения между шинами грузового автомобиля и дорогой k=0.2? Силой трения качения, действующей на легковой автомобиль и массой колес, пренебречь.
Решение: Проекция сил, действующих на систему из двух автомобилей, на направление их движения равна: (M+m)a = kMgcos a – Mgsin a – mgsin a.
Отсюда а = g( Mkcos a /M+m – sin a )= 0,6 м/с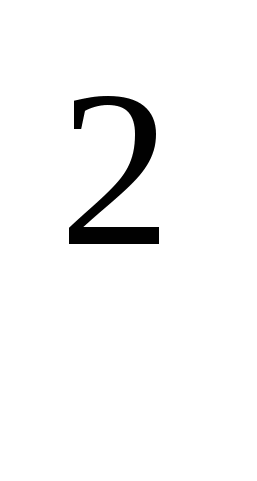
Р
5 уровень — качественные задачи
1. Докажите, что крупные капли дождя падают быстрее, чем мелкие. Капли имеют форму шара, силу сопротивления воздуха считать пропорциональной площади поперечного сечения капли.
Решение: Сила тяжести, действующая на каплю, пропорциональна ее обьему, т.е. кубу радиуса капли. Сила сопротивления со стороны воздуха пропорциональна площади поперечного сечения, т.е. квадрату радиуса капли. Таким образом, с ростом массы капли
сила тяжести растет быстрее силы сопротивления воздуха, и крупные капли движутся вниз с большим ускорением.
Деревянный брусок плавает на поверхности воды в миске. Миска покоится на поверхности земли. Что произойдет с глубиной погружения бруска в воду, если миска будет стоять на полу лифта, который движется с ускорением , направленным вертикально вверх?
Решение: 1.Когда брусок, вода и миска покоятся относительно Земли, сила Архимеда уравновешивает силу тяжести плавающего бруска. Та же по величине и направлению сила Архимеда уравновешивает силу тяжести вытесненной бруском воды. Поэтому масса бруска и масса вытесненной им воды одинаковы.
Когда брусок, вода и миска покоятся относительно друг друга, но движутся с ускорением относительно Земли, одна и та же сила Архимеда вместе с силой тяжести сообщает одно и то же ускорение как плавающему бруску, так и воде в объеме, вытесненном бруском, что приводит к соотношению:
F= m(a- g) = m1(a- g), где m – масса бруска, а m1 – масса вытесненной воды, откуда следует, что и при движении относительно Земли с ускорением отличным от g масса бруска и масса вытесненной им воды одинаковы.
Поскольку масса бруска одна и та же, масса вытесненной им воды в обоих случаях одинакова. Вода практически не сжимаема, поэтому плотность воды в обоих случаях одинакова. Значит, объем вытесненной воды не изменяется, глубина погружения бруска в лифте остается прежней.
3.Тело брошено под углом к горизонту. Что займет больше времени: подъем или спуск. Учесть сопротивление воздуха.
Решение: В каждой точке траектории силу сопротивления можно разложить на две составляющие: горизонтальную и вертикальную. Горизонтальная составляющая не оказывает влияния на время движения, а только изменяет дальность полета. Вертикальная составляющая влияет на время подъема и падения, так как на восходящей части траектории совпадает с направлением силы тяжести, а на нисходящей части направлена противоположно ей. Для всех точек, находящихся на одинаковой высоте на восходящей и нисходящей ветвях траектории, численное значение ускорения будет больше для восходящей ветви и меньше для нисходящей, поэтому время подъема будет меньше времени спуска.
Список литературы
Комплекты учебников/ Под ред. Г. Я. Мякишев, Б. Б. Буховцев, Н.Н. Сотский
Н. И. Зорин Элективный курс « Методы решения физических задач». 10-11 классы
Физика ЕГЭ — 2013 под редакцией Л. М. Монастырского
Различные сборники физических задач.
