определение, алгоритм и методы решения, примеры
В математике большая часть задач ориентирована на решение стандартных уравнений, в которых представлена одна переменная. Однако, некоторые из них, помимо числовых выражений, содержат одновременно две неизвестные. Перед тем как приступить к решению такого уравнения, стоит изучить его определение.
Определение
Итак, уравнением с двумя неизвестными называют любое равенство следующего типа:
a*x + b*y =с, где a, b, c — числа, x, y — неизвестные переменные.
Ниже приведены несколько примеров:
- 10x + 25y = 180.
- x — y = 6.
- -6x + y = 7.
Уравнение с двумя неизвестными точно так же, как и с одной, имеет решение. Однако такие выражения, как правило, имеют бесконечное множество разных решений, поэтому в алгебре их принято называть неопределенными.
Решение задач
Чтобы решить подобные задачи, необходимо отыскать любую пару значений x и y, которая удовлетворяла бы его, другими словами, обращала бы уравнение с неизвестными x и y в правильное числовое равенство. Найти удовлетворяющую пару чисел можно при помощи метода подбора.
Для наглядности объяснений подберем корни для выражения: y-x = 6.
При y=5 и x=-1 равенство становится верным тождеством 5- (-1) = 6. Поэтому пару чисел (-1; 5) можно считать корнями выражения y-x = 6. Ответ: (-1; 5).
Необходимо отметить, что записывать полученный ответ по правилам необходимо в скобках через точку с запятой. Первым указывается значение х, вторым — значение y.
У равенств такого вида может и не быть корней. Рассмотрим такой случай на следующем примере: x+y = x+y+9
Приведем исходное равенство к следующему виду:
В результате мы видим ошибочное равенство, следовательно, это выражение не имеет корней.
При решении уравнений можно пользоваться его свойствами. Первое их них: каждое слагаемое можно вынести в другую часть выражения. Вместе с этим обязательно нужно поменять знак на обратный. Получившееся равенство будет равнозначно исходному.
Например, из выражения 20y — 3x = 16 перенесем неизвестное y в другую его часть.
- 20y — 3x = 16;
- -3x = 16−20y.
Оба равенства равносильны.
Второе свойство: допустимо умножать или делить части выражения на одинаковое число, не равное нолю. В итоге получившиеся равенства будут равнозначны.
Пример:
- y — x = 6*2;
- 2y — 2x = 12.
Оба уравнения также равносильны.
Система уравнений с двумя неизвестными
Система уравнений представляет собой некоторое количество равенств, выполняющихся одновременно. В большинстве задач приходится находить решение системы, состоящей из двух равенств с двумя переменными.
Для решения системы уравнений необходимо найти
Решить подобные системы уравнений можно, применяя следующие методы.
Метод подстановки
Последовательность действий:
- Выражаем неизвестное из любого равенства через вторую переменную.
- Подставляем получившееся выражение неизвестного во второе равенство и решаем его.
- Делаем подстановку полученного значения неизвестного и вычисляем значение второго неизвестного.
Метод сложения
Этапы решения:
- Приводим к равенству модули чисел при каком-либо неизвестном.
- Производим вычисление одной из переменных, произведя сложение или вычитание полученных выражений.
- Подставляем найденное значение в какое-либо уравнение в первоначальной системе и вычисляем вторую переменную.
Графический метод
- Выражаем в каждом равенстве одну переменную через другую.
- Строим графики двух имеющихся уравнений в одной координатной плоскости.
- Определяем точку их пересечения и ее координаты. На этом шаге у вас может получиться три варианта: графики пересекаются — у системы единственно верный вариант решения; прямые параллельны друг другу — система решений не имеет; графики совпадают — у системы бесконечно много решений.
- Делаем проверку, подставив полученные значения в исходную систему равенств.
При нахождении корней у одной системы всеми этими способами у вас обязательно должен получиться одинаковый результат, если вы, конечно, все сделали правильно.
В настоящее время есть возможность решения подобных задач с помощью встроенных средств офисной программы Excel, а также на специализированных онлайн-ресурсах и калькуляторах. С помощью них вы легко можете проверить правильность своих вычислений и результатов.
Надеемся, что наша статья помогла вам в освоении этой базовой темы школьной математики. Если же вы пока не можете справиться с решением уравнений такого вида, не расстраивайтесь. Для понимания и закрепления изученной темы рекомендуется как можно больше практиковаться, и тогда у вас без труда получится решать задачи любой сложности. Желаем вам удачи в покорении математических вершин!
Видео
Из этого видео вы узнаете, как решать уравнения с двумя неизвестными.
задачи с двумя переменными, задача с двумя неизвестнами, axmara.narod.ru о математике.
Мой племянник опять не может решить задачу!
Давайте вместе попробуем решить несколько задач с двумя неизвестными!
Уясните для себя самое главное! Не бойтесь математику! Полюбите её! И вы будете щелкать эти задачи как семечки! Ведь математика – это самая главная наука!
И неважно, что эта задача не похожа на вашу, если вы не научитесь решать их самостоятельно, то любое изменение условия задачи, будет всегда для вас проблемой!
Условие задачи с двумя неизвестными :
Миша сказал, что одна лента в 2 раза длиннее, чем вторая.
А Оля сказала, что одна лента длиннее другой на 3см.
Решение задачи с двумя неизвестными:
Правильное решение задачи с двумя переменными зависит от правильности составления уравнений!
Большую ленту выразим через – х.
Маленькую выразим через – у.
Слова Миши можно записать как х = 2у.
Слова Оли можно записать как х – у = 3.
У нас получилось 2 уравнения с двумя неизвестными.
Заменим во втором уравнении х на 2у, ведь х = 2у.
И получим 2у – у = 3, у = 3.
Подставим у = 3, в первое уравнение х = 2*х=6.
Ответ к задаче с двумя неизвестными:
Первая лента равна 6см, а вторая 3см.
Написать что-нибудь…
задачи с двумя переменными , решить задачу два велосипедиста . задачи с двумя неизвестными , задача два автомобиля выехали одновременно , задача два пешехода вышли одновременно , задача две трубы ,примеры, объяснение. Задачи по алгебре :: SYL.ru
Рано или поздно любому школьнику на уроках алгебры встречаются задачи, решаемые с помощью уравнения. Поначалу появление букв вместо привычных цифр и действия с ними ставят в тупик даже самых одарённых, но если разобраться, всё далеко не так сложно, как кажется на первый взгляд.
Алгоритм решения
Перед тем как перейти к конкретным примерам, необходимо понять алгоритм решения задач с помощью уравнений. В любом уравнении есть неизвестное, чаще всего обозначаемое буквой Х. Также и в каждой задаче есть то, что необходимо найти, то же самое неизвестное. Именно его и нужно обозначать как Х. А потом, следуя условию задачи, прибавлять, отнимать, умножать и делить – совершать любые необходимые действия.
После нахождения неизвестного обязательно выполнение проверки, чтобы быть уверенными, что задача решена правильно. Стоит заметить, что дети уже в начальной школе начинают решение задач с помощью уравнений. Примеры этому — те задачи, которые нужно решать отрезками, являющимися полнейшими аналогами буквенных неизвестных.
Основа основ — задача про корзины
Итак, попробуем же на практике применить решение задач с помощью уравнений, объяснение алгоритма которых было дано чуть выше.
Дана задача: Собрали некоторое количество корзин с яблоками. Сначала 3 корзины продали, потом дособирали ещё 8 корзин. В итоге получилось 12 корзин. Сколько корзин яблок собрали первоначально?
Начнём решение задачи с того, что обозначим неизвестное — то есть первоначальное количество корзин – буквой Х. Теперь начинаем составлять уравнение: Х (первоначальное количество) – 3 (проданные корзины) + 8 (те, которые собрали позже) = 12 (итоговое число корзин), то есть Х — 3 + 8 = 12. Решив простое уравнение, получим, что Х = 7. Обязательно выполняем проверку, то есть подставляем найденное число в равенство: 7 — 3 + 8 действительно равно 12, то есть задача решена верно.
Закрепление: концертные залы
Дана следующая задача: В двух концертных залах 450 мест. Известно, что в одном зале мест в 4 раза больше, чем в другом. Нужно узнать, сколько мест в каждом зале.
Для того чтобы решать подобные задачи по алгебре, снова нужно применить уравнение. Мы знаем, что сумма двух чисел, одно из которых в 4 раза больше другого, равна 450. Пусть число мест в меньшем зале, неизвестное, будет равно Х, тогда число мест в большем зале – 4 * Х = 4Х. Следовательно, 450 = Х + 4Х = 5Х. А дальше нужно решить стандартное уравнение 450 = 5Х, где Х = 450 / 5 = 90, то есть в меньшем зале 90 мест, значит в большем – 90 * 4 = 360. Чтобы убедиться, что задача решена правильно, можно проверить неравенство: 360 + 90 = 450, то есть ответ верный.
Классика: полки с книгами
Но задачи, решаемые с помощью уравнения, могут быть и посложнее. Например, есть три полки с книгами. На первой полке книг на 8 больше, чем на второй, а на третьей — в 3 раза больше, чем на второй, причём количество книг на первой и третьей полках равное. Сколько книг на каждой полке?
Понятно, что отталкиваться здесь нужно от второй полки, которая встречается в обоих условиях. Если мы обозначаем количество книг на ней за Х, то тогда на первой полке Х + 8 книг, а на третьей — Х * 3 книг, при этом Х + 8 = 3Х. Решив уравнение, получаем Х = 4. Выполняем проверку, подставляя неизвестное в равенство: 4 + 8 действительно равно 3 * 4, то есть задача решена правильно.
Практикуемся дальше: бобры
Как видите, решение задач с помощью уравнения гораздо легче, чем кажется на первый взгляд. Закрепим навыки работы с уравнениями ещё одной задачей. Первый бобр сгрыз за день какое-то количество деревьев. Второй бобр сгрыз в 6 раз больше. Третий бобр сгрыз в 2 раза больше деревьев, чем первый, но в 3 раза меньше, чем второй. Сколько деревьев сгрыз каждый бобр?
Задача не такая запутанная, какой кажется на первый взгляд. Для начала найдём неизвестное – в этой задаче это количество деревьев, сгрызенных первым бобром. Следовательно, второй бобр уничтожил 6 * Х деревьев, а третий – 2 * Х, причём это число в 3 раза меньше 6 * Х. Составляем уравнение: 6Х = 3 * 2Х. Решив его, получаем, что первый бобр погрыз всего одно дерево, тогда второй – 6, а третий – 2. Подставив числа в уравнение, понимаем, что задача решена верно.
Соотносим уравнения и условия
Если вам скажут: «К каждой задаче подберите соответствующее уравнение», — не пугайтесь – это целиком и полностью реально.
Даны следующие уравнения:
- 6 + Х = 2Х;
- 6 = 2Х;
- 2 + Х = 6.
Условия задач следующие:
- У мальчика было 6 яблок, а у девочки в два раза меньше, сколько было яблок у девочки?
- На столе лежат ручки и карандаши, известно, что ручек на столе 6, а карандашей на 2 меньше, сколько ручек и сколько карандашей на столе?
- У Вани на шесть монет больше, чем у Тани, а у Тани в два раза меньше, чем у Ани, сколько монет у каждого ребёнка, если у Вани и Ани одинаковое количество монет?
Составим уравнения по каждой из задач.
- В первом случае нам не известно число яблок у девочки, то есть оно равно Х, мы знаем, что Х в 2 раза меньше 6, то есть 6 = 2Х, следовательно, к этому условию подходит уравнение №2.
- Во втором случае за Х обозначается количество карандашей, тогда количество ручек Х + 2, но при этом мы знаем, что ручек 6, то есть Х + 2 = 6, значит сюда подходит третье уравнение.
- Что касается последней задачи, под номером 3, количество Таниных монет, которое встречается в двух условиях, является искомым неизвестным, тогда у Вани 6 + Х монет, а у Ани 2Х монет, то есть 6 + Х = 2Х – очевидно, что сюда подходит первое уравнение.
Если у вас есть задачи, решаемые с помощью уравнения, к которым необходимо подобрать соответствующее равенство, то составьте уравнение для каждой из задач, а потом уже соотносите то, что получилось у вас, с данными уравнениями.
Усложняем: система уравнений — конфеты
Следующий этап применения буквенных равенств в алгебре – это задачи, решаемые системой уравнений. В них имеется два неизвестных, причём одно из них выражается через другое на основании имеющихся данных. Известно, что у Паши и Кати вместе 20 конфет. Ещё известно, что если бы у Паши было на 2 конфеты больше, то у него было бы 15 конфет, сколько конфет у каждого?
В данном случае мы не знаем ни количество Катиных конфет, ни количество Сашиных конфет, следовательно, у нас два неизвестных, Х и Y соответственно. Вместе с тем, мы знаем, что Y + 2 = 15.
Составив систему, получаем два уравнения:
- Х + Y = 20;
- Y + 2 = 15.
А дальше действуем по правилам решения систем: выводим Y из второго уравнения, получая Y = 15 — 2, а потом подставляем его в первое, то есть Х + Y = Х + (15 — 2) = 20. Решив уравнение, получаем Х = 7, тогда Y = 20 — 7 = 13. Проверяем правильность решения, подставив Y во второе уравнение: 13 + 2 действительно равно 15, то есть у Кати 7 конфет, а у Паши — 13.
Ещё сложнее: квадратные уравнения и земельный участок
Встречаются также и задачи по алгебре, решаемые квадратным уравнением. В них нет ничего сложного, просто стандартная система преобразовывается в квадратное уравнение в ходе решения. Например, дан участок земли площадью в 6 гектаров (60000 квадратных метров), забор, огораживающий его, имеет длину 1000 метров. Каковы длина и ширина участка?
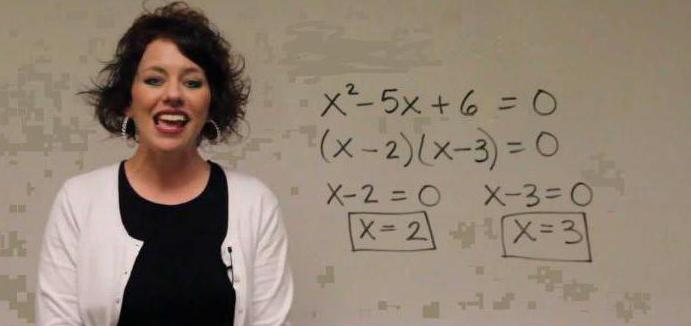
Составляем уравнения. Длина забора является периметром участка, следовательно, если длину обозначить Х, а ширину Y, то 1000 = 2 * (Х + Y). Площадь же, то есть Х * Y = 60000. Из первого уравнения выводим Х = 500 — Y. Подставляя его во второе уравнение, получаем (500 — Y) * Y = 60000, то есть 500Y — Y2 = 60000. Решив уравнение, получаем стороны равные 200 и 300 метрам – квадратное уравнение имеет два корня, один из которых зачастую не подходит по условию, например, является отрицательным, тогда как ответ должен быть числом натуральным, поэтому проверку проводить обязательно.
Повторяем: деревья в саду
Закрепляя тему, решим ещё одну задачу. В саду есть несколько яблонь, 6 груш и несколько вишнёвых деревьев. Известно, что общее количество деревьев в 5 раз больше, чем количество яблонь, при этом вишневых деревьев в 2 раза больше, чем яблоневых. Сколько деревьев каждого вида в саду и сколько в саду всего деревьев?
За неизвестное Х, как, наверное, уже понятно, обозначаем яблоневые деревья, через которые мы сможем выразить остальные величины. Известно, что Y = 2X, а Y + Х + 6 = 5Х. Подставив Y из первого уравнения, получаем равенство 2Х + Х + 6 = 5Х, откуда Х = 3, следовательно в саду Y = 3 * 2 = 6 вишнёвых деревьев. Проводим проверку и отвечаем на второй вопрос, складывая получившиеся величины: 3 + 6 + 6 = 3 * 5, то есть задача решена верно.
Контрольная: сумма чисел
Решение задач с помощью уравнения далеко не такое сложное, как кажется на первый взгляд. Главное – не ошибиться в выборе неизвестного и, что ещё важнее, правильно его выразить, особенно если речь идёт о системе уравнений. В завершение даётся последняя задача, гораздо более запутанная, чем представленные выше.
Сумма трёх чисел – 40. Известно, что Х = 2Y + 3Z, а Y = Z — 2 / 3. Чему равны Х, Y и Z?
Итак, начнём с избавления от первого неизвестного. Вместо Х подставляем в равенство соответствующее выражение, получаем 2Y + 3Z + Z + Y = 3Y + 4Z = 40. Далее заменяем также известный Y, получая равенство 3Z — 2 + 4Z = 40, откуда Z = 6. Возвращаясь к Y, находим, что он равен 5.2, а Х, в свою очередь, равен 18. С помощью проверки убеждаемся в истинности выражения, следовательно задача решена правильно.
Заключение
Итак, что же такое задачи, решаемые с помощью уравнения? Так ли они страшны, как кажется на первый взгляд? Ни в коем случае! При должной усидчивости разобраться в них не составляет никакого труда. А однажды поняв алгоритм, в дальнейшем вы сможете щёлкать подобные задачки, даже самые запутанные, как семечки. Главное – внимательность, именно она поможет правильно определить неизвестное и путём решения порой множества уравнений найти ответ.
Решение задач на нахождение неизвестного по двум разностям
В мастерской сшили одинаковые плащи из двух кусков ткани (см. рис. 1). В одном куске было на 4 метра ткани больше, и из него сшили на 2 плаща больше. Сколько ткани расходовали на 1 плащ?
Запишем условие задачи в таблицу 1:
— первая графа в таблице – это расход ткани на 1 плащ. Так как сшили одинаковые плащи, то расход ткани на каждый плащ будет одинаковым;
— вторая графа таблицы – это количество плащей. Нам неизвестно, сколько плащей сшили из каждого куска ткани, но известно, что из большего куска сшили на два плаща больше;
— третья графа – общий расход ткани. Нам неизвестно, сколько ткани было в каждом куске, но известно, что один кусок ткани на 4 метра больше другого.
Табл. 1. Условие задачи
Решение
Нам известны две разности: одна разность показывает, что плащей сшили на 2 больше, другая разность показывает, что один кусок ткани на 4 метра больше другого.
Почему из одного куска ткани сшили на 2 плаща больше? Потому что этот кусок ткани больше на 4 метра. Можно сделать вывод, что на 2 плаща расходовали 4 метра ткани. Для того чтобы найти, сколько ткани расходуют на 1 плащ, необходимо 4 разделить на 2:
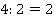(м)
Ответ: на один плащ расходовали 2 м ткани.
В мастерской сшили одинаковые плащи из двух кусков ткани длиной 6 метров и 10 метров (см. рис. 2). Из большего куска сшили на 2 плаща больше. Сколько плащей сшили из каждого куска?
Рис. 2. Иллюстрация к задаче
Запишем условие задачи в таблицу 2:
— первая графа в таблице – это расход ткани на 1 плащ. Так как сшили одинаковые плащи, то расход ткани на каждый плащ будет одинаковым;
— вторая графа таблицы – это количество плащей. Нам неизвестно, сколько плащей сшили из каждого куска ткани, но известно, что из большего куска сшили на два плаща больше;
— третья графа – общий расход ткани. Нам известно, что один кусок ткани имеет длину 6 метров, а второй кусок – 10 метров.
Табл. 2. Условие задачи
Решение
1. Для того чтобы узнать, сколько плащей сшили из каждого куска ткани, необходимо знать, сколько ткани расходуют на 1 плащ.
Расход ткани на один плащ можно найти по двум разностям. Однако нам дана только одна разность – это разность количества плащей. Вторую разность (разность длин тканей) необходимо найти. Для этого из длины большего куска ткани нужно вычесть длину меньшего куска:
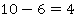(м)
2. Теперь нам известна и вторая разность, которая показывает, что один кусок ткани на 4 метра длиннее другого.
Если один кусок ткани на 4 метра длиннее другого и плащей из этого куска сшили на два больше, то можно сделать вывод, что на 2 плаща расходовали 4 метра ткани. Для того чтобы найти, сколько ткани расходуют на 1 плащ, необходимо 4 разделить на 2:
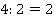(м)
3. Нам известен расход ткани на один плащ, – это 2 метра, и длина ткани в одном куске – это 6 метров, то можно найти, сколько из этого куска ткани сшили плащей:
(п)
4. Другой кусок ткани имеет длину 10 метров, поэтому можно найти, сколько из этого куска ткани сшили плащей:
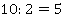(п)
Ответ: из одного куска ткани сшили 3 плаща, а из другого – 5 плащей.
Список литературы
1. Математика. Учебник для 4 кл. нач. шк. В 2 ч./М.И. Моро, М.А. Бантова. – М.: Просвещение, 2010.
2. Демидова Т.Е., Козлова С.А., Тонких А.П. Математика. 4 класс. Учебник в 3 ч. 2-е изд., испр. – М.: 2013.; Ч. 1 – 96 с., Ч. 2 – 96 с., Ч. 3 – 96 с.
3. Узорова О.В., Нефедова Е.А. Большой задачник по математике. 4 класс. – М.: 2013. – 256 с.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Интернет-сайт ppt4web.ru (Источник)
2. Интернет-сайт «Инфоурок» (Источник)
3. Интернет-сайт «Мои лекции» (Источник)
Домашнее задание
1. Задачи 178, 180 (стр. 37) – Математика. Учебник для 4 кл. нач. шк. В 2 ч./М.И. Моро, М.А. Бантова (Источник)
2. Два автомобиля ехали с одинаковой скоростью. Один из них проехал 400 км, а другой – 480 км. Сколько часов был в пути каждый автомобиль, если первый был в пути на 2 часа меньше, чем второй?
3. Два шофера возили зерно. Один из них сделал 3 рейса, другой – 5 рейсов за день. Второй шофер перевез на 30 т зерна больше, чем первый. Сколько зерна перевез каждый из шоферов по отдельности, если каждый рейс перевозилось одинаковое количество зерна?
Линейное уравнение с двумя переменными и его график (более сложные случаи)
На данном уроке мы научимся решать более сложные задачи, в которых речь идет о линейных уравнениях с двумя неизвестными. Мы закрепим технику решения данных уравнений и построения графиков, вспомним теоретические основы и добавим к ним некоторые факты.
Напомним, что линейным уравнением с двумя переменными называется уравнение вида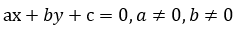 
Мы научились строить графики подобных уравнений и узнали, что они имеют бесчисленное множество решений – пар чисел х и у, которые на графике отображаются в виде точек.
В предыдущих задачах нам было задано уравнение, но как и все другие – линейное уравнение с двумя переменными это математическая модель некоторой реальной ситуации. Теперь рассмотрим такие задачи, в которых нужно для простейшей задачи составить уравнение – математическую модель, а затем его решить.
Пример 1:
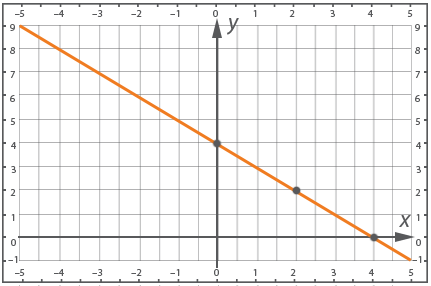
Сумма двух чисел равна четырем. Построить математическую модель, то есть соответствующее линейное уравнение, и его график.
Пусть искомые числа это х и у, сумма их равна четырем:
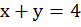
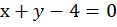– линейное уравнение с двумя переменными. Построим график, для этого составим таблицу, для контроля возьмем три точки, а не две:
Решение задачи сведено в таблицу:
|
Словесная модель |
Сумма двух чисел равна четырем |
|
Алгебраическая модель |
|
|
Геометрическая модель |
|
Следующая группа задач связана с тем, что в одной задаче могут участвовать два линейных уравнения.
Пример 2:
Графически найти точку пересечения прямых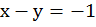 
и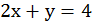 
Обе прямые являются графиками соответствующих уравнений, построим их. Для этого составим таблицы. Для удобства представим уравнение в следующем виде:
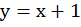
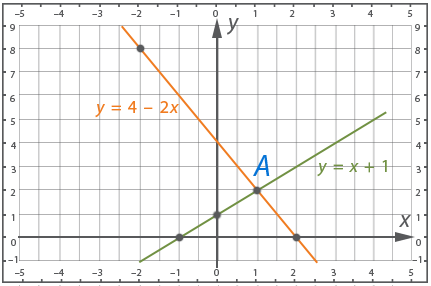
Графически найдена точка пересечения А(1; 2)
Чтобы проверить, что точка А(1; 2) удовлетворяет обоим уравнениям, нужно подставить ее координаты в уравнения:
;
точка А удовлетворяет обоим уравнениям, значит, точка пересечения прямых найдена верно.
Следующий тип задач – это задачи с параметрами.
Пример 3:
Найдите значение коэффициента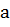 
в уравнении 
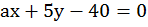, если известно, что решением уравнения является пара чисел (3; 2)
Ранее у нас было задано или мы сами составляли линейное уравнение с известными коэффициентами, в данном случае один из коэффициентов неизвестен, но дано одно из решений уравнения, то есть пара значений х и у, удовлетворяющих уравнению. Чтобы найти параметр 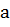подставим данные значения в уравнение:
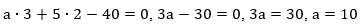
итак, исходное уравнение имеет вид: 
Итак, мы рассмотрели линейное уравнение с двумя неизвестными:
Отметим, что в случае, если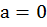 
, мы получаем частный случай данного уравнения – уравнение с одной переменной:
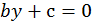
Аналогично если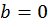 
мы получим линейное уравнение с одной переменной:
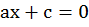
Вывод: в данном уроке мы рассмотрели более сложные задачи на линейные уравнения с двумя переменными, в частности текстовые задачи, уравнения с параметрами, задачи на два уравнения. Кроме того мы закрепили знание понятий и терминов.
Список рекомендованной литературы
1. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. М.: Просвещение. 2010 г.
2. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. М.: ВЕНТАНА-ГРАФ
3. Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7 .М.: Просвещение. 2006 г.
Рекомендованные ссылки на ресурсы интернет
1. Интернет-портал Nado5.ru (Источник).
2. Портал для семейного просмотра (Источник).
3. Интернет-портал Nado5.ru (Источник).
Рекомендованное домашнее задание
Задание 1: Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7, № 980, ст.212;
Задание 2: Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7, № 981, ст.212;
Задание 3: Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7, № 986, ст.212;
Решение задач с помощью составления систем уравнений
Решая задачи при помощи уравнений, мы искали, как правило, одно неизвестное. Но встречаются и задачи, где есть несколько неизвестных. Такие задачи принято решать посредством составления систем уравнений.
Задача 1.
Навстречу друг другу из одного города в другой, расстояние между которыми составляет 30 км, едут два велосипедиста. Предположим, что если велосипедист 1 выедет на 2 ч раньше своего товарища, то они встретятся через 2,5 часа после отъезда велосипедиста 2; если же велосипедист 2 выедет 2мя часами ранее велосипедсита 1, то встреча произойдет через 3 часа после отъезда первого. С какой скоростью движется каждый велосипедист?
Решение.
1. Определим скорость велосипедиста 1 как х км/ч, а скорость велосипедиста 2 как у км/ч.
2. Если первый велосипедист выедет на 2 ч раньше второго, то, согласно условию, он будет ехать до встречи 4,5 ч, тогда как второй 2,5 часа. За 4,5 ч первый проедет путь 4,5х км, а за 2,5 ч второй проедет путь 2,5у км.
3. Встреча двух велосипедистов означает, что суммарно они проехали путь 30 км, т.е. 4,5х + 2,5 у = 30. Это и есть наше первое уравнение.
4. Если второй выедет на 2 ч раньше первого, то, согласно условию, он будет ехать до встречи 5 ч, тогда как первый – 3 ч. Используя рассуждения, аналогичные изложенным выше рассуждениям, приходим к уравнению:
3х + 5у = 30.
5. Итак, мы получили систему уравнений
{4,5х + 2,5 у = 30,
{3х + 5у = 30.
6. Решив полученную систему уравнений, мы найдем корни: х = 5, у = 3.
Т.о., первый велосипедист едет со скоростью 5 км/ч, а второй – 3 км/ч.
Ответ: 5 км/ч, 3 км/ч.
Задача 2.
Вкладчику на его сбережения через год было начислено 6 $ процентных денег. Добавив 44 $, вкладчик оставил деньги еще на год. По истечении года вновь было произведено начисление процентов, и теперь вклад вместе с процентами составил 257,5 $. Какая сумма составляла вклад первоначально и сколько процентов начисляет банк?
Решение.
1. Пусть х ($) – первоначальный вклад, а у (%) – это проценты, которые начисляются ежегодно.
2. Тогда к концу года к первоначальному вкладу добавится (у/100) ∙ х $.
Из условия получаем уравнение (ух/100) = 6.
3. По условию известно, что в конце года вкладчик внес еще 44 $, так что вклад в начале второго года составил х + 6 + 44, т.е. (х + 50) $. Таким образом, сумма, полученная к концу второго года с учетом начисления, равнялась (х + 50 + (у/100)(х + 50)) $. По условию эта сумма равна 275,5 $. Это позволило нам составить второе уравнение:
х + 50 + (у/100)(х + 50) = 257,5
4. Итак, мы получили систему уравнений:
{(ух/100) = 6,
{х + 50 + (у/100)(х + 50) = 257,5
После преобразования системы уравнений мы получим:
{ху = 600,
{100х + 50у + ху = 20750.
Решив систему уравнений, мы нашли два корня: 200 и 1,5. Только первое значение удовлетворяет нашему условию.
Подставим значение х в уравнение и найдем значение у:
если х = 200, то у = 3.
Таким образом, первоначальный вклад составлял 200 $, а банк в год производит начисление а размере 3 %.
Ответ: 200 $; 3 %.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра
Нелинейные уравнения с двумя неизвестными
Определение 1. Пусть A – некоторое множество пар чисел (x ; y) . Говорят, что на множестве A задана числовая функция z от двух переменных x и y , если указано правило, с помощью которого каждой паре чисел из множества A ставится в соответствие некоторое число.
Задание числовой функции z от двух переменных x и y часто обозначают так:
причем в записи (1) числа x и y называют аргументами функции, а число z – значением функции, соответствующим паре аргументов (x ; y) .
Определение 2. Нелинейным уравнением с двумя неизвестными x и y называют уравнение вида
где f (x , y) – любая функция, отличная от функции
f (x , y) = ax +by + c ,
где a , b , c – заданные числа.
Определение 3. Решением уравнения (2) называют пару чисел (x ; y) , для которых формула (2) является верным равенством.
Пример 1. Решить уравнение
| x2 – 4xy + 6y2 – – 12 y +18 = 0 . | (3) |
Решение. Преобразуем левую часть уравнения (3):
x2 – 4xy + 6y2 – 12 y +18 =
= (x2 – 4xy + 4y2) +
+ (2y2– 12y +18) =
= (x – 2y)2 + 2(y – 3)2 .
Таким образом, уравнение (3) можно переписать в виде
| (x – 2y)2 + 2(y – 3)2 = 0 . | (4) |
Поскольку квадрат любого числа неотрицателен, то из формулы (4) вытекает, что неизвестные x и y удовлетворяют системе уравнений
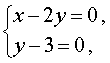
решением которой служит пара чисел (6 ; 3) .
Ответ: (6 ; 3)
Пример 2. Решить уравнение
Решение. Из неравенства
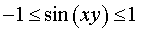
вытекает, что уравнение (5) решений не имеет.
Ответ: Решений нет.
Пример 3. Решить уравнение
Решение. В соответствии с определением логарифма из формулы (6) получаем
Следовательно, решением уравнения (6) является бесконечное множество пар чисел вида
(1 + y ; y) ,
где y – любое число.
Системы из двух уравнений, одно из которых линейное
Определение 4. Решением системы уравнений
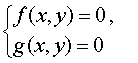
называют пару чисел (x ; y) , при подстановке которых в каждое из уравнений этой системы получается верное равенство.
Системы из двух уравнений, одно из которых линейное, имеют вид
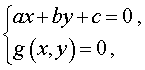
где a , b , c – заданные числа, а g(x , y) – функция двух переменных x и y .
Пример 4. Решить систему уравнений
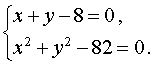 | (7) |
Решение. Выразим из первого уравнения системы (7) неизвестное y через неизвестное x и подставим полученное выражение во второе уравнение системы:
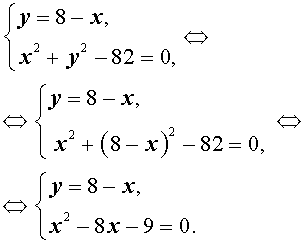
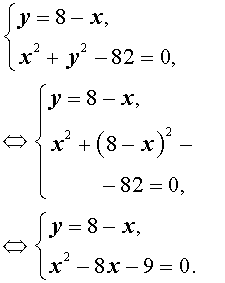
Решая уравнение
x2 – 8x – 9 = 0 ,
находим корни
x1 = – 1 , x2 = 9 .
Следовательно,
y1 = 8 – x1 = 9 ,
y2 = 8 – x2 = – 1 .
Таким образом, решениями системы (7) являются две пары чисел
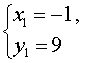и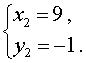 
Ответ: (– 1 ; 9) , (9 ; – 1)
Однородные уравнения второй степени с двумя неизвестными
Определение 5. Однородным уравнением второй степени с двумя неизвестными x и y называют уравнение вида
ax2 + bxy + cy2 = 0 .
где a , b , c – заданные числа.
Пример 5. Решить уравнение
| 3x2 – 8xy + 5y2 = 0 . | (8) |
Решение. Для каждого значения y рассмотрим уравнение (8) как квадратное уравнение относительно неизвестного x . Тогда дискриминант D квадратного уравнения (8) будет выражаться по формуле
D = (8y)2 – 60y2 = 4y2 ,
откуда с помощью формулы для корней квадратного уравнения найдем корни уравнения (8):
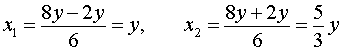
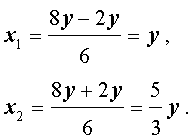
Ответ. Решениями уравнения (8) являются все пары чисел вида
( y ; y) или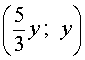 
где y – любое число.
Следствие. Левую часть уравнения (8) можно разложить на множители
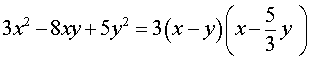
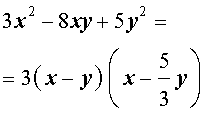
Системы из двух уравнений, одно из которых однородное
Системы из двух уравнений, одно из которых однородное, имеют вид
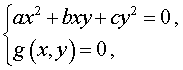
где a , b , c – заданные числа, а g(x , y) – функция двух переменных x и y .
Пример 6. Решить систему уравнений
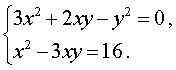 | (9) |
Решение. Решим однородное уравнение
3x2 + 2xy – y2 = 0 ,
рассматривая его как квадратное уравнение относительно неизвестного x :
.
В случае, когда x = – y , из второго уравнения системы (9) получаем уравнение
4y2 = 16 ,
корнями которого служат числа y1 = 2 , y2 = – 2 . Находя для каждого из этих значений y соответствующее ему значение x , получаем два решения системы: (– 2 ; 2) , (2 ; – 2) .
В случае, когда
,
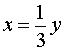из второго уравнения системы (9) получаем уравнение
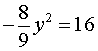
которое корней не имеет.
Ответ: (– 2 ; 2) , (2 ; – 2)
Системы из двух уравнений, сводящиеся к системам, в которых одно из уравнений однородное
Пример 7. Решить систему уравнений
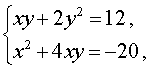 | (10) |
Решение. Совершим над системой (10) следующие преобразования:
- второе уравнение системы оставим без изменений;
- к первому уравнению, умноженному на 5 , прибавим второе уравнение, умноженное на 3 , и запишем полученный результат вместо первого уравнения системы (10).
В результате система (10) преобразуется в равносильную ей систему (11), в которой первое уравнение является однородным уравнением:
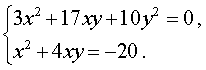 | (11) |
Решим однородное уравнение
3x2 + 17xy + 10y2 = 0 ,
рассматривая его как квадратное уравнение относительно неизвестного x :
.
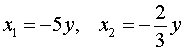В случае, когда x = – 5y , из второго уравнения системы (11) получаем уравнение
5y2 = – 20 ,
которое корней не имеет.
В случае, когда
,
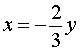из второго уравнения системы (11) получаем уравнение
,
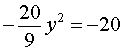корнями которого служат числа y1 = 3 , y2 = – 3 . Находя для каждого из этих значений y соответствующее ему значение x , получаем два решения системы: (– 2 ; 3) , (2 ; – 3) .
Ответ: (– 2 ; 3) , (2 ; – 3)
Примеры решения систем уравнений других видов
Пример 8. Решить систему уравнений (МФТИ)
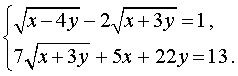  | (12) |
Решение. Введем новые неизвестные u и v , которые выражаются через x и y по формулам:
 | (13) |
Для того, чтобы переписать систему (12) через новые неизвестные, выразим сначала неизвестные x и y через u и v . Из системы (13) следует, что
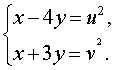 | (14) |
Решим линейную систему (14), исключив из второго уравнения этой системы переменную x . С этой целью совершим над системой (14) следующие преобразования:
- первое уравнение системы оставим без изменений;
- из второго уравнения вычтем первое уравнение и заменим второе уравнение системы на полученную разность.
В результате система (14) преобразуется в равносильную ей систему
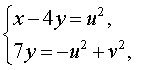
из которой находим
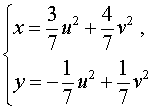 | (15) |
Воспользовавшись формулами (13) и (15), перепишем исходную систему (12) в виде
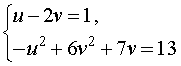 | (16) |
У системы (16) первое уравнение – линейное, поэтому мы можем выразить из него неизвестное u через неизвестное v и подставить это выражение во второе уравнение системы:
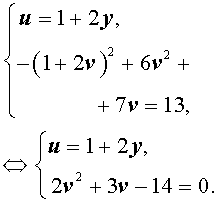
Решая уравнение
2v2 + 3v – 14 = 0 ,
находим корни
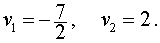
Следовательно, решениями системы (16) являются две пары чисел
Из формул (13) вытекает, что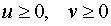 
, поэтому первое решение должно быть отброшено. В случае u2 = 5, v2 = 2 из формул (15) находим значения x и y :
x = 13, y = – 3 .
Ответ: (13 ; – 3)
Определение 6. Решением системы из двух уравнений с тремя неизвестными называют тройку чисел (x ; y ; z) , при подстановке которых в каждое уравнение системы получается верное равенство.
Пример 9. Решить систему из двух уравнений с тремя неизвестными
 | (17) |
Решение. У системы (17) первое уравнение – линейное, поэтому мы можем выразить из него неизвестное z через неизвестные x и y и подставить это выражение во второе уравнение системы:
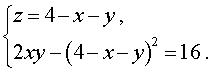 | (18) |
Перепишем второе уравнение системы (18) в другом виде:
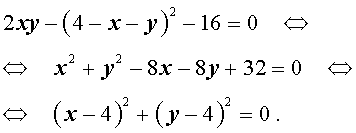
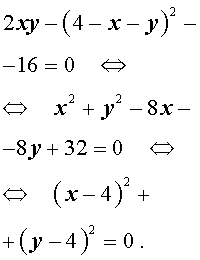
Поскольку квадрат любого числа неотрицателен, то выполнение последнего равенства возможно лишь в случае x = 4, y = 4 .
Следовательно,
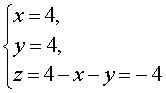
Ответ: (4 ; 4 ; – 4)
Замечание. Рекомендуем посетителю нашего сайта, интересующемуся методами решения систем уравнений, ознакомиться также c разделом справочника «Системы линейных уравнений» и нашим учебным пособием «Системы уравнений».
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.