Tg x tgx: Функция y=tgx, ее свойства и график . Видеоурок. Алгебра 10 Класс – Функции y=tgx, ctg x. Их свойства и графики

Функция y=tgx, ее свойства и график . Видеоурок. Алгебра 10 Класс

Тема: Тригонометрические функции

Урок: Функция y=tgt, её свойства и график

Напоминание:

Определение: Функцией 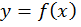называется закон, по которому каждому допустимому значению  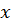ставится в соответствие единственное значение y.

Множество всех точек координатной плоскости 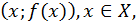 называется графиком функции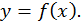

На отрезке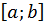

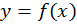 задана функция  (рис. 1).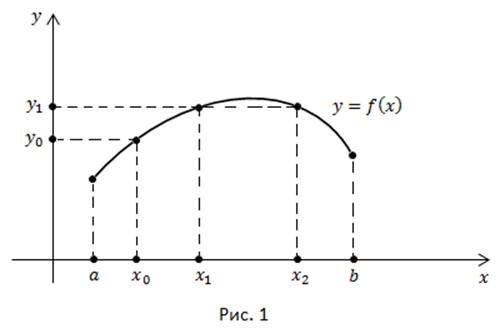

По определению, каждому значению 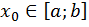 ставится в соответствие только одно значение  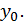И обратно: значение функции  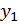может достигаться при нескольких значениях аргумента: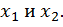

Дадим определение функци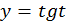и  или  .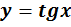

Нам важен закон, по которому каждому значению 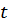 ставится в соответствие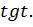  

Зададим произвольное 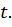 Значение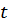

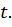 откладывается на числовой окружности по часовой стрелке либо против часовой стрелки, в зависимости от знака  Получаем единственную точку M с единственной парой координат (рис. 2).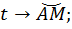

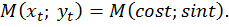
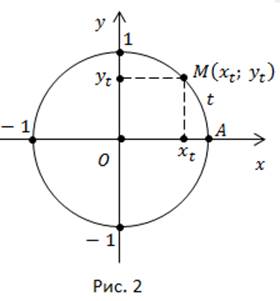
Координату  называют косинусом числа

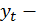 координату  синусом числа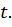

Тангенсом числа 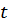 называется отношение синуса  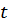к косинусу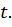

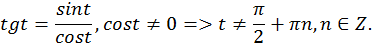
Нам известно, что каждому значению аргумента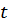

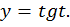 ставится в соответствие единственное значение функции  Покажем это графически.

Проведем касательную к числовой окружности в точке A. Заданному значению 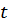 соответствует единственная точка M, единственная прямая OM и единственная точка T пересечения прямой OM и касательной (рис. 3).

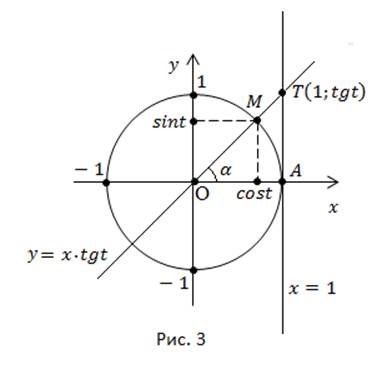
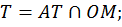
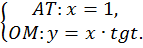
Наша цель – найти координаты точки T, для этого решим систему уравнений.

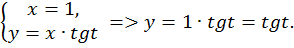
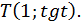
Ордината точки 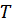 равна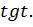  

Прямую 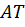 называют линией тангенсов.

Докажем, что область значений тангенса – это все действительные числа,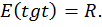

Доказательство:

Зададим любое действительное значение 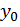 и докажем, что оно достигается хотя бы при одном значении аргумента.

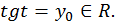
Отложим 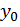 на линии тангенсов, получим точку  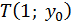(рис. 4).

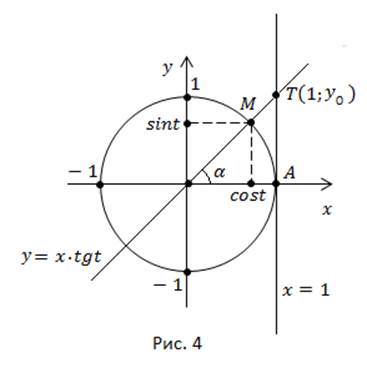
Соединим её с точкой O, получим прямую 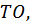 которая пересекает числовую окружность хотя бы в одной точке M, а, значит, существует единственная дуга  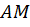и хотя бы одно значение  которое равно длине дуги.

Любому действительному значению аргумента соответствует единственное значение функции. Но любому значению функции соответствует хотя бы одно значение аргумента.

Таким образом, мы задали любое значение функции и доказали, что оно достигается хотя бы при одном значении аргумента.

Отметим два важных свойства функции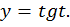

1. Нечетность функции.

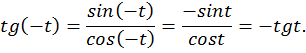
Т.е.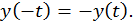

2. Докажем, что период функции равен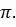

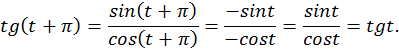
Таким образом, для любого значения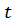 выполняется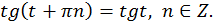

Эти свойства функции 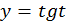 позволяют нам легко построить её график. Период функции равен  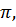значит, мы можем  изучить её свойства и построить график на любом участке длиной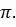

Нечетность функции позволяет симметрично отобразить участок графика относительно начала координат.

С учетом этого построим график функции 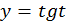 на промежутке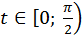

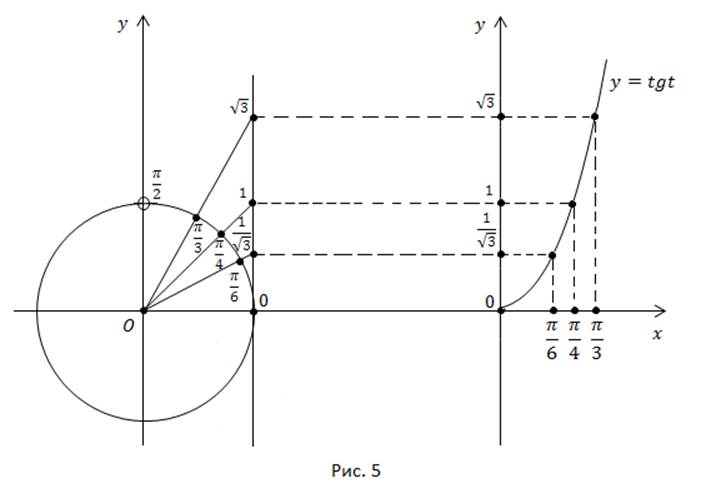
 (рис. 5).

Мы получили график функции на заданном промежутке. Можно было построить график и по известным табличным значениям. Например:

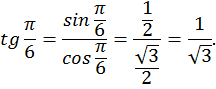
Из построенного графика функции на промежутке 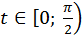 видно, что функция возрастает. Докажем это.

Рассмотрим график 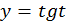 на промежутке  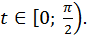Точки 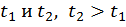 (рис. 6).

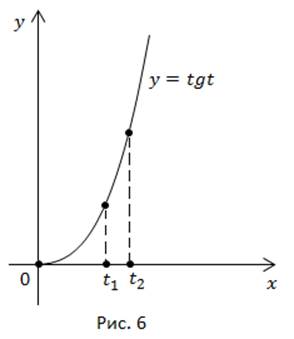
Докажем, что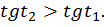

Доказательство:

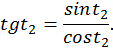
На промежутке 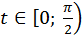 функция  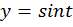возрастает, значит  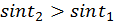(рис. 7).

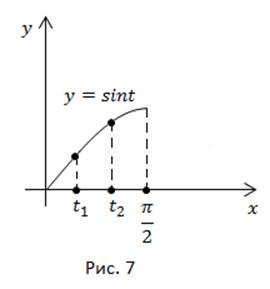
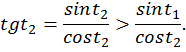
На промежутке 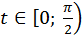 функция  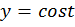убывает, значит  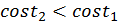(рис. 8).

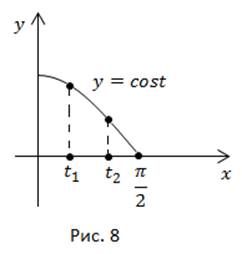
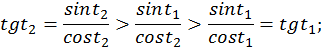
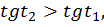  значит, функция  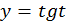возрастает на промежутке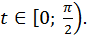

Зная свойства функции, мы можем построить её график на всей области определения.

В точках 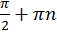  проходят вертикальные асимптоты (рис. 9).

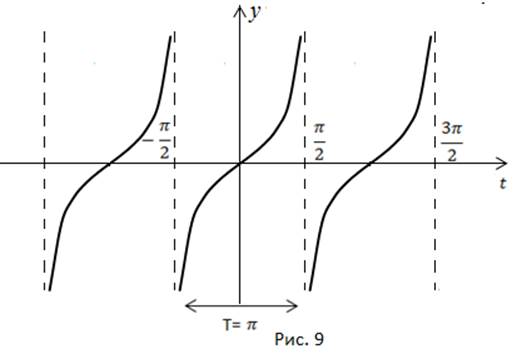
Рассмотрим основные свойства функции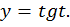

1) Область определения: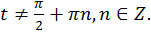

2) Функция периодическая с периодом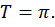

3) Функция нечетная.

4) Функция возрастает и непрерывна на любом интервале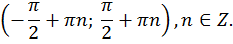

5) Функция не ограничена.

6) Функция не имеет ни минимального, ни максимального значения.

7) 

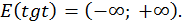
Задача.  Решить уравнение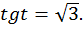

Функции y=tgx, ctg x. Их свойства и графики

Вопросы занятия:

·     рассмотреть тангенс и котангенс как функции аргумента x;

·     познакомиться с основным свойствам функций y=tg x, ctg x;

·     построить графики функций y=tg x, ctg x.

Материал урока.

Для того, чтобы найти область определения функции y = tg x давайте ещё раз вспомним определение тангенса x.

Найдём область значений функции y = tg x.

Найдём период функции y = tg x. И исследуем её на чётность.

Поскольку функция y = tg x – периодичная функция с периодом π, то можно построить график функции на промежутке [-π/2; π/2], а затем сдвинуть построенную ветвь влево и вправо на π, 2π, 3π и  так далее.

Поскольку функция нечётная, то можно построить на промежутке [0; π/2] и отобразить относительно начала координат.

Для построения графика на промежутке [0; π/2], составим таблицу значений тангенса для основных точек из этого промежутка. Отметим эти точки на координатной плоскости.

Отобразим полученную часть графика относительно начала координат.

Сдвинем построенную ветвь влево и вправо на π.

По построенному графику легко определить основные свойства функции y = tg x.

Исследование на монотонность.

Исследование на ограниченность.

Наибольшее и наименьшее значение функции.

Исследование на непрерывность.

Давайте, ещё раз перечислим все свойства функции y = tg x.

Проведя аналогичные рассуждения, можно построить график функции   y = ctg x на промежутке [0; π], затем отразить симметрично относительно начала координат и сдвинуть получившуюся ветвь влево и вправо.

Давайте, перечислим все свойства функции y = ctg x.

Решите уравнение tg^2 x + 5tgx + 6 = 0.. — Задание 13 ЕГЭ по математике (Уравнения)

Задание:

а) Решите уравнение tg²x + 5tgx + 6 = 0
б) Найдите все корни этого уравнения, принадлежащие отрезку [-2π;-π/2]

Решение:

 

а) tg²x + 5tgx + 6 = 0

Для удобства заменим тангенс на t. (tgx = t), тогда

t² + 5t + 6 = 0

Получили обычное квадратное уравнение. Найдем корни уравнения по теореме Виета: (можно искать и через дискриминант, кому как удобно):

t₁ + t₂ = -5
t₁ * t₂ = 6

Получаем, что:

t₁ = -2
t₂ = -3

(через дискриминант вы получите те же t₁ и t₂)

Делаем обратную замену, то есть заменим t на тангенс:

tgx = t₁                                  tgx = t₂
tgx = -2                                  tgx = -3

Отсюда:

x = -arctg2 + πn, n Є Z           x = -arctg3 + πk, k Є Z

б) Сделаем замену для подбора корней: (-arctg2 и  -arctg3 — это приблизительно -π/3)
x = -π/3 + πn, n Є Z            x = -π/3 + πk, k Є. Z

Выходит, что у этих уравнений одинаковые корни, решим только одно из них:

x = -π/3 + πn, n Є Z

Воспользуемся методом перебора n, для нахождения корней.

Пусть n = 0, подставляем в x:
x = -π/3 + π * 0 = -π/3 + 0 = -π/3 — Не принадлежит нашему отрезку [-2π;-π/2];

Пусть n = -1
x = -π/3 + π *(-1) = -π/3 — π = -4π/3 — Принадлежит нашему отрезку  [-2π;-π/2];

Больше корней нет, делаем обратную замену -π/3 на -arctg2 и  -arctg3, получаем при n = -1:
-arctg2 — π; -arctg3 — π

Ответ: а) x = -arctg2 + πn, n Є Z.
                     x = -arctg3 + πk, k Є Z.
                  б) -arctg2 — π ; -arctg3 — π.

Ответы Mail.ru: (tgx+tg2x)/1-tgxtg2x=1 помогите решить

(tgx+tg2x)/(1-tgxtg2x)=1 делаем преобразование tgx+tg2x / 1-tgxtg2x= — tg2x+tgx / tgxtg2x — 1 уравниваем — tg2x + tg x / tgxtg2x -1 =1 применяем основн тиронометрич тождество -(cosxsin2x + sinxcos2x) / (sinxsin2x — cosxcos 2x)=1 периодические решения 2пи к /3 + пи/12 2пи к/3 — пи/4 ответ: х принадежит (2пи к /3 + пи/12 2пи к/3 — пи/4) где к принадлежит Z

tg 3x=1 <img src=»//otvet.imgsmail.ru/download/28011942_489cfd007e3c0dda1a7787320f08e505_800.png» alt=»» data-lsrc=»//otvet.imgsmail.ru/download/28011942_489cfd007e3c0dda1a7787320f08e505_120x120.png» data-big=»1″>

Нужно воспользоваться формулой: (tgα+tgβ)/(1-tgαtgβ)=tg(α+β) И далее по формуле корней: tgx=a x=arctg a + πn, n∈Z